Accelerazione
Calcolo alternativo
Metodo a tabella
Piccoli spostamenti
Implementazione
Variazione dinamica
TB6560
DRV8825
Download
In giro per internet si trovano un sacco di schemi di circuiti di controllo per motori passo-passo, unitamente a schede e azionamenti gia' pronti per l'uso, quindi non mi dilunghero' sull'argomento: supponiamo di aver acquistato un driver per motori passo-passo e che questo funzioni perfettamente.
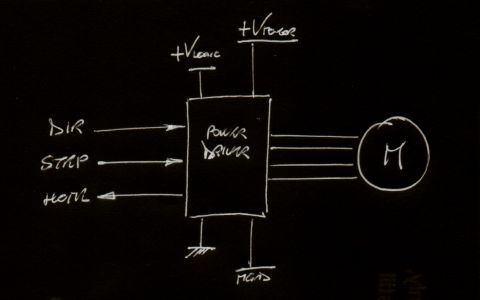
Driver per motori passo passo
Supponiamo inoltre di aver scelto uno schema di pilotaggio a passo intero, niente wave drive, niente micro stepping, anche se questi possono essere considerati come dettagli marginali. Il nocciolo della questione riguarda la frequenza degli impulsi, a che velocita' pilotiamo il nostro motore?
Per rispondere correttamente a questa domanda dobbiamo considerare la natura dei motori passo-passo: il motore e' caratterizzato, come tutti i motori, da una curva velocita'-coppia; come la maggior parte dei motori elettrici anche i motori passo-passo presentano una curva discendente: all'aumentare della velocita' la coppia erogata dal motore decresce fino ad esaurirsi completamente.
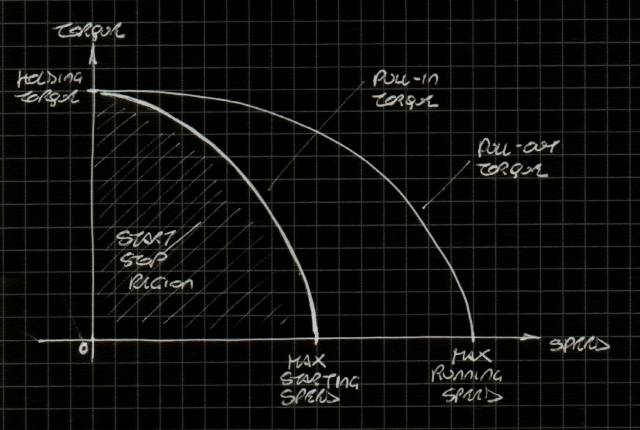
Grafico velocita'-coppia
Per complicare le cose il grafico del motore passo-passo e' doppio: presenta due curve, una chiamata pull-in torque e una chimata pull-out torque. La prima delle due racchiude un'area denominata start/stop region nel grafico sopra. Un motore passo-passo si avvia sempre se la frequenza degli impulsi e' all'interno della start/stop region.
La curva pull-in torque tocca l'asse orizzontale alla max starting speed, questa e' la massima velocita' alla quale e' possibile avviare il motore da fermo. Da notare che a questa velocita' la coppia e' nulla, quindi il motore potrebbe riuscire ad avviarsi, ma sicuramente non sotto sforzo.
Una volta avviato il motore puo' essere accelerato fino a toccare la curva di pull-out, questa e' la coppia massima erogabile dal motore, oltre il motore collassa, perde il sicronismo col campo magnetico rotante e si ferma ronzando alla frequenza degli impulsi di controllo.
Questa breve descrizione ci fa intuire che: mantenedosi al di sotto della curva di pull-in possiamo pilotare il motore a frequenza fissa senza problemi, non raggiungeremo grandi velocita' ma difficilmente finiremo col perdere dei passi. Inoltre se vogliamo raggiungere velocita' elevate (rimane pur sempre un motore passo-passo) dobbiamo accelerare correttamente il motore fino alla velocita' desiderata.
Un'ultima nota: una volta accelerato il motore va anche decelerato, fermare di colpo gli impulsi al di sopra della curva di pull-in potrebbe portare ad una perdita dei passi: se il motore non riesce a fermarsi all'istante, prosegue nel suo moto per un numero imprecisato di passi, disallineandosi dal sistema di controllo.
Accelerazione
Tralasciamo quindi il pilotaggio a frequenza costante e cerchiamo una tecnica per modificare la frequenza degli impulsi. Beninteso: il pilotaggio a frequenza costante non va cassato completamente, e' molto utile nel caso di movimenti lenti o molto piccoli in cui risulta inutile accelerare e decelerare.
Con una dose di fantasia notevole possiamo dire che la cosa piu' semplice che si possa immaginare consiste nell'accelerare costantemente fino a velocita' massima, quindi mantenere la velocita' costante fino all'approssimarsi della destinazione e decellerare costantemente fino a fermarsi con precisione micrometrica nel punto di arresto prescelto. Il grafico qui sotto chiarisce la situazione.
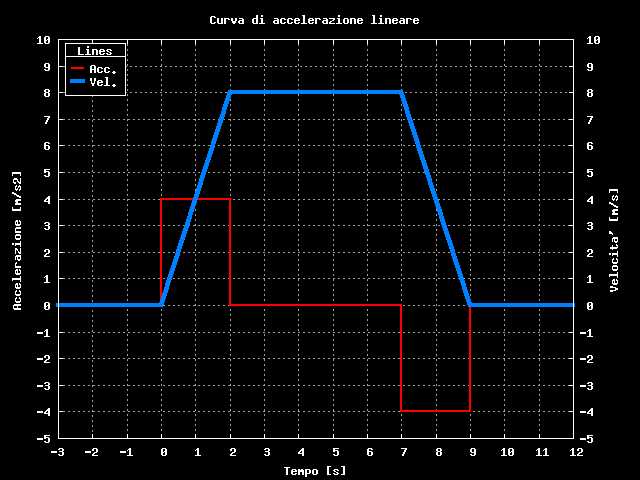
Accelerazione e velocita' nel tempo
Fissiamo le regole del gioco: consideriamo di possedere un oscillatore che generi una frequenza di riferimento fck, questa frequenza base viene divisa per un valore intero c generando la frequenza dei passi. Quindi variando opportunamente il divisore c possiamo variare la frequenza dei passi, quindi la velocita' del motore.
I dati da cui partiamo sono: la frequenza base fck, l'ampiezza del passo del motore alfa e l'accelerazione angolare che vogliamo dare al motore a.

Rifacciamo il grafico sopra riportando solo la velocita' angolare del motore e suddividendo l'asse temporale in opportuni intervalli Delta-t. Lo scopo del gioco e' proprio trovare la giusta sequenza degli intervalli Delta-t che fanno si che l'accelerazione angolare del motore sia costante e pari al valore desiderato.
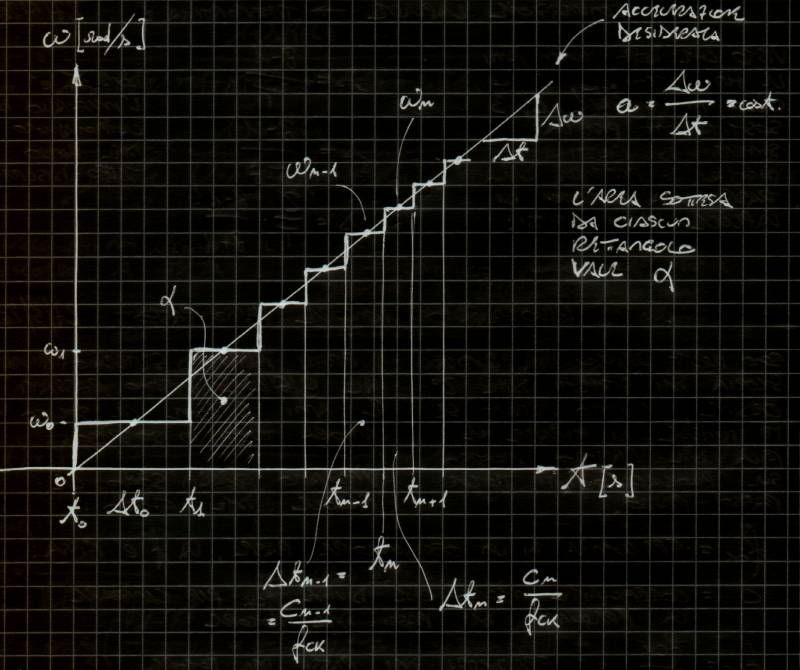
Suddivisione dell'asse temporale
Consideriamo ora un istante temporale generico t(n) che divide due passi del motore, il passo precedente (alla sinistra di t(n)) inizia all'istante t(n-1) e ha durata Delta-t(n-1). All'istante t(n) inizia un nuovo passo di durata Delta-t(n) che portera' fino all'istante t(n+1).
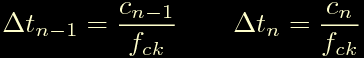
Nel grafico sopra ogni rettangolo ha area pari ad alfa, per cui la velocita' angolare (che viene ritenuta costante all'interno di tutto il passo) nel passo n-esimo vale:
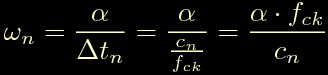
Girando l'ultima otteniamo l'espressione di c(n):
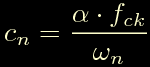
Ora dovremmo riuscire a sostituire omega(n) ed esprimerlo in funzione di omega(n-1), seguendo la definizione stessa di velocita' otteniamo:
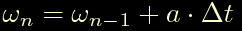
Qui scatta il dubbio amletico: quale periodo scegliere come Delta-t in questa formula?
La mia prima scelta e' stata:
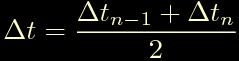
basata sulla distanza tra i punti medi degli impulsi riportati sul grafico sopra. Purtroppo con questa sostituzione non riesco a risolvere l'equazione.
Internet invece consiglia di considerare come intervallo di tempo l'intero impulso precedente: di fatto nel tempo Delta-t(n-1) si passa da velocita' omega(n-1) a velocita' omega(n), quindi sostituiamo:
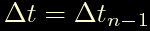
ed otteniamo:
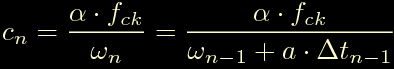
In questa sostituiamo:
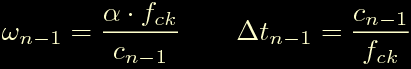
ed otteniamo:
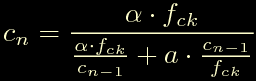
Da qui con un po' di giri si ottiene:
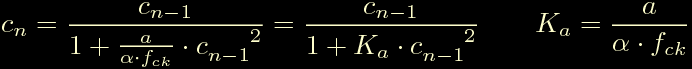
Questa formula permette di calcolare il c n-esimo dinamicamente mentre il moto procede, conosciuto il precedente. Ora non resta altro che calcolare il primo coefficiente c0, per fare questo ricominciamo da:

Facendo alcune considerazioni geometriche intorno al primo passo possiamo scrivere:
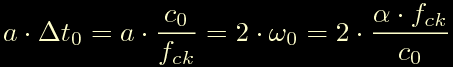
da cui si ottiene:
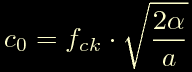
Riassumendo possiamo calcolare la sequenza dei divisori di frequenza come:
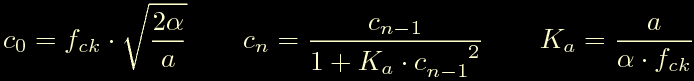
Dopo tutte queste elugubrazioni su accelerazioni, intervalli temporali e voli pindarici assortiti, direi di infilare questa formule in un calcolatore e verificare se funzionano veramente. La simulazione fatta con un programmino C produce questi risultati:
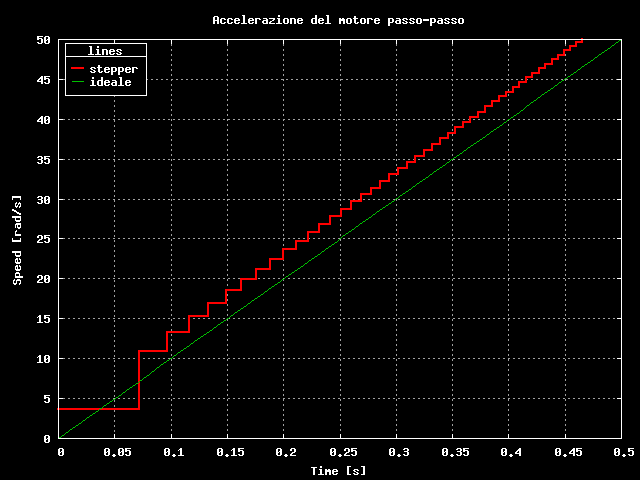
Verifica accelerazione motore
Per quanto la curva risulti temporalmente sfalsata, l'inclinazione e' corretta, quindi abbiamo ottenuto il nostro scopo: ora siamo in grado di accelerare il motore passo-passo con accelerazione costante. Per decelerare lo stesso motore si una la stessa formula, e' sufficiente considerare l'accelerazione negativa.
Calcolo alternativo
Il discorso potrebbe essere finito qui, se non fosse per tutte quelle radici quadrate ed elevamenti a potenza. Il dubbio che mi viene e': "Esiste un modo piu' semplice per calcolare la sequenza dei c(n)?"
Ripartiamo dalle origini: l'equazione del moto uniformemente accelerato:
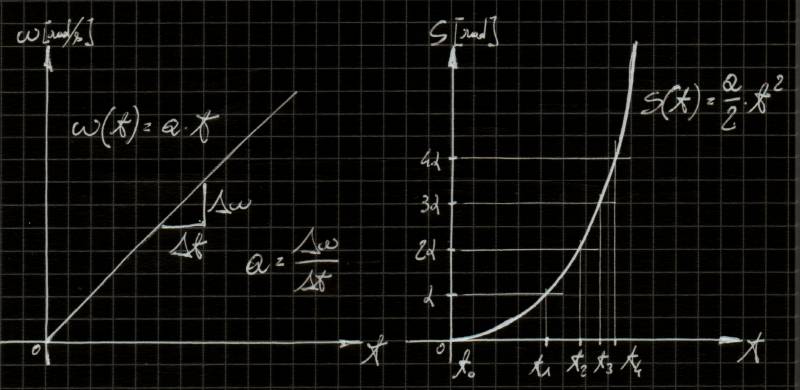
Moto uniformemente accelerato
Istante per istante la posizione angolare del motore vale:
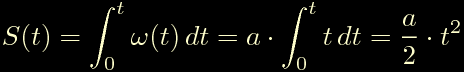
Noi siamo interessati ai particolari istanti tn per cui lo spazio S risulta un multiplo intero di alfa.
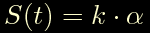
Nel nostro mondo dominato dall'indice n la riscriviamo in questo modo:

dopo di che sostituiamo la definizione di S(t) ed otteniamo gli istanti tn:
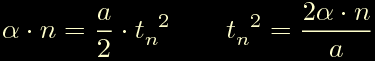
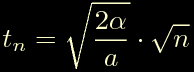
Questi sono gli istanti di tempo che ci interessano, ora basta ricordarsi che:
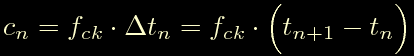
sostituiendo tn si ottiene in fine:
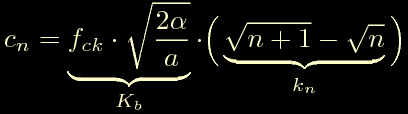
Questa vorrebbe essere la forma non ricorsiva che permette di calcolare i coefficienti cn partendo dall'indice n. Da notare che Kb e' una costante che dipende dalle caratteristiche del motore stesso e dall'accelerazione angolare alla quale vogliamo sottoporlo, mentre i coefficienti kn rappresentano una successione costante per qualunque motore. Se facciamo un bel grafico otteniamo questo andamento:
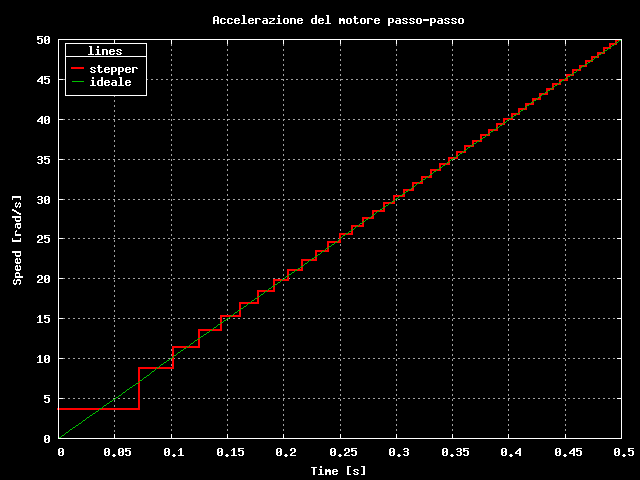
Verifica accelerazione motore
PERFETTO!!!
Questa volta non c'e' nemmeno quel piccolo spostamento temporale che
poteva lasciare qualche dubbio sull'affidabilita' del metodo.
Certo qualcuno potrebbe obiettare il fatto che le radici quadrate non sono scomparse, e' vero, ma adesso io gioco il jolly: come si vede sopra i coefficienti cn sono il prodotto di una parte costante Kb e di una sequenza kn. Il primo dipende solo dalle caratteristiche del motore e quindi puo' essere calcolato una volta per tutte all'inizio del movimento. Il secondo e' una sequenza di coefficienti che non dipende dal motore ne dal moto e che quindi potrebbe essere contenuta in una tabella.
Questo secondo metodo di calcolo apre la possibilita' di avere un metodo a tabella. Solitamente non smanio per i metodi a tabella perche' richiedono sempre una discreta quantita' di memoria che preferisco non sprecare, certo dall'altra parte semplificano e velocizzano notevolmente i calcoli, cose che in questa circostanza piena di radici quadrate potrei apprezzare molto.
Metodo a tabella
Prima di addentrarci nella questione facciamo un bel confronto dei risultati fin qui ottenuti, non tanto perche' serva veramente a qualcosa, ma perche' ho gia' preparato il grafico e quindi devo metterlo da qualche parte, mi sembra il momento buono.
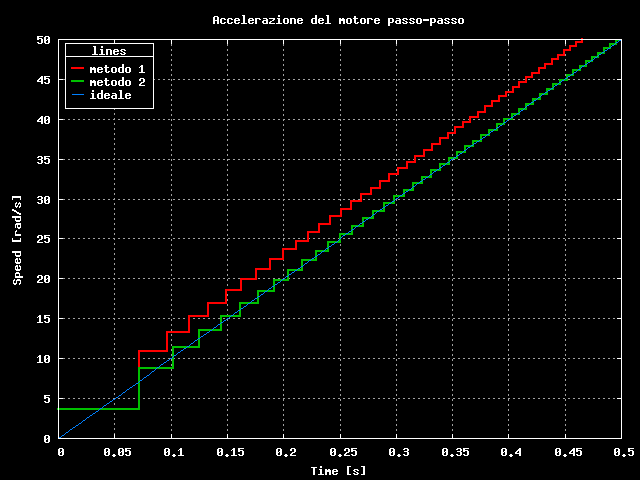
Confronto accelerazione motore
Ora che ci siamo divertiti riprendiamo l'espressione dei cn vista sopra:
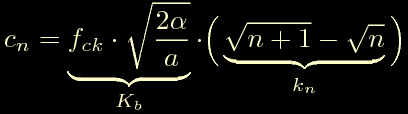
La costante Kb puo' essere calcolata una volta per tutte, o quantomeno solo quando cambia l'accelerazione angolare. Purtroppo il calcolo di Kb include una radice quadrata, almeno per il momento cerchiamo di non farne un dramma, ritorneremo poi su questa questione.
La successione dei kn e' sempre la stessa per ogni motore, quindi possiamo farne una tabella e non dovremo mai piu' calcolarli, solo prelevarli dalla tabella e con un solo prodotto ottenere il nostro cn. Fare una tabella di dimensione chiaramente finita pone pero' dei problemi: l'accelerazione del motore non potra' durare in eterno, prima o poi la tabella finira' e se il motore non avra' raggiunto la velocita' finale saremo nei pasticci.
In realta' la soluzione pacifica consiste nel dire che se la tabella finisce il motore cessa, per forza di cose, la rampa di accelerazione e prosegue a velocita' costante, qualunque velocita' abbia raggiunto. Se non ha raggiunto la velocita' desiderata se ne fa una ragione e se la mette via cosi'. Il problema comunque rimane: quanto facciamo lunga la tabella per non rischiare di dover segare tutte le rampe di accelerazione?
Rispondiamo prima ad un'altra domanda: "Che velocita' si raggiunge
accelerando uniformemente per N passi?"
Inoltre: "Quanto tempo ci abbiamo messo?"
Ripartiamo dall'equazione del moto:
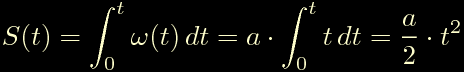
Ora consideriamo gli istanti di tempo tN per cui l'integrale della velocita' e' multiplo intero di alfa:
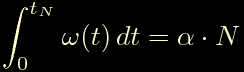
Sostituendo atteniamo:
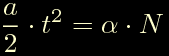
da cui risolvendo per t si ottiene:
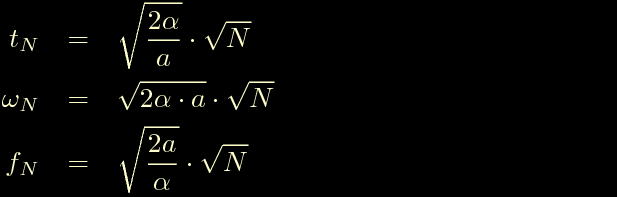
Questa sono rispettivamente: il tempo necessario per eseguire i primi N impulsi, la velocita' angolare e la frequenza degli impulsi raggiunta dopo N passi.
Ora prendiamo l'ultima ed eleviamo al quadrato entrambi i membri, si ottiene:
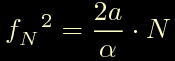
in cui sostituiamo alfa con:
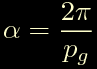
in cui pg rappresenta i passi giro, un po' piu' maneggevole dell'ampiezza del passo singolo. Riarrangiando i membri e risolvendo rispetto all'accelerazione angolare otteniamo:

Chiameremo questa accelerazione limite.
L'accelerazione limite non costituisce un limite invalicabile,
indica solo il valore di accelerazione al di sotto del quale il
motore non e' piu' in grado di raggiungere la frequenza massima degli
impulsi fmax. Questa limitazione e' chiaramente imposta dalla
dimensione della tabella dei kn, indicata come Nmax
nella formula di sopra.
Questo e' in buona sostanza il limite a cui si va incontro avendo una tabella di coefficienti finita. Ben'inteso che non e' un vincolo per il motore dover raggiungere sempre la frequenza massima degli impulsi, ora la domanda che tutti si fanno e': "Ma quanto vale questa accelerazione limite? E' tanto o e' poco?"
Per tentare di rispondere alla domanda ho fatto un paio di grafici ipotizzando due tabelle di coefficienti: una con 256 coefficienti ed una con 512.
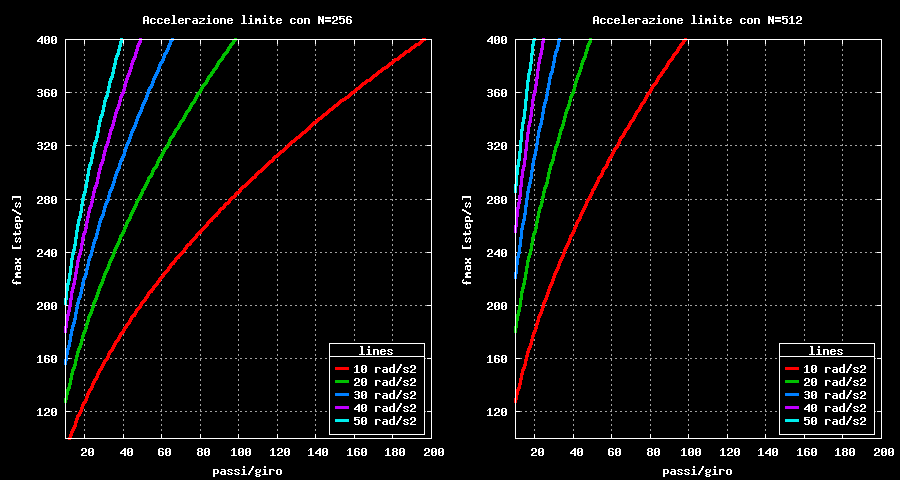
Accelerazione limite per il metodo a tabella
Consideriamo per semplicita' il grafico di destra, quello con N pari a 256, il grafico si legge nel seguente modo: consideriamo un motore da 100 passi/giro, individuiamo quindi il 100 sull'asse delle ascisse e saliamo fino ad incontrare la curva dei 10 rad al secondo quadrato, troviamo che corrisponde a circa 280 impulsi al secondo. Ora se avviassimo questo motore con un'accelerazione inferiore a 10 rad/s2 allora non riusciremmo piu' ad arrivare alla frequenza di 280 impulsi/s perche' la tabella dei coefficienti finirebbe prima. Secondo questi discorsi una tabella da 512 coefficienti rischierebbe di diventare corta solo per motori con molti impulsi/giro e accelerazioni veramente basse (pochi rad/s2); di fatto il grafico comprende la frequenza di 400 impulsi/s, una frequenza degli impulsi veramente alta per un motore passo-passo.
Per tentare di capire meglio quali siano i limiti possiamo fare un grafico diverso: il grafico qui sotto riporta sulla sisnistra la velocita' raggiunta dopo N passi da fermo, in particolare sono riportate le curve a 256, 512 e 1024 passi.
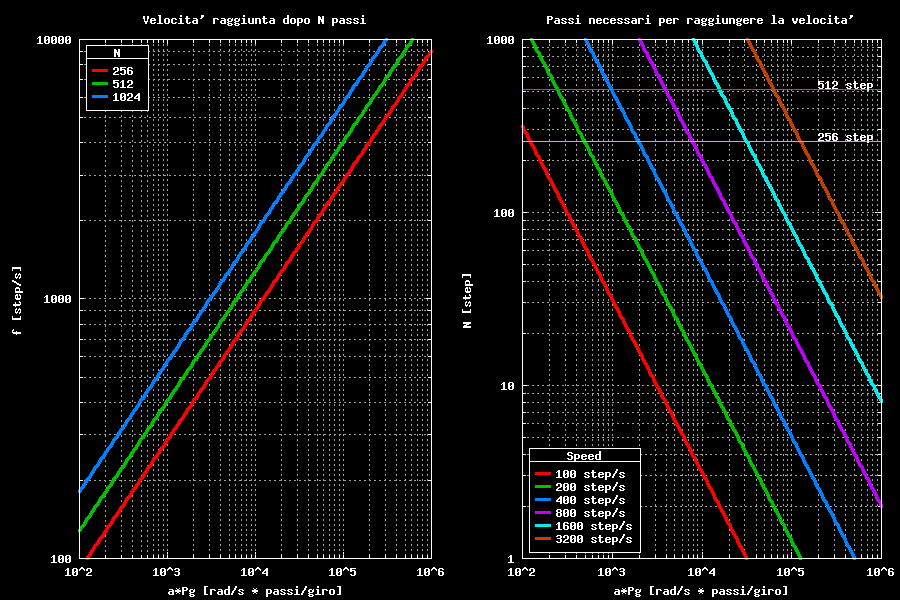
Verifica della lunghezza della tabella dei coefficienti Kn
Per verificare che la tabella dei coefficienti Kn sia sufficientemente lunga scegliere il prodotto a * Pg sull'asse delle x, salire fino ad incontrare la curva relativa alla nostra tabella (nel nostro caso la riga verde), quindi osservare sull'asse verticale la velocita' massima raggiungibile. Se il grafico riporta una velocita' superiore alla velocita' massima che intendiamo raggiungere (la velocita' massima e' dettata dal sistema meccanico non dal driver) allora la tabella dei Kn e' sufficientemente lunga. Usando questo grafico e' possibile confrontare le diverse tabelle tra loro.
Il grafico a destra invece permette di valutare l'accelerazione: il grafico permette di calcolare il numero di passi necessari per raggiungere la velocita' massima da fermo, questo permette di valutare sia la scelta dell'accelerazione che la dimensione della tabella dei coefficienti Kn.
Le versioni stampabili di questi grafici sono disponibili qui.
Virgola fissa
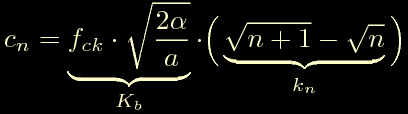
Tutti i kn tranne il primo sono inferiori a 1 (ma sempre maggiori di 0), k0 vale 1. Al contrario, tutti i cn sono ben maggiori di 1: ricordo che questo e' il divisore della frequenza base generata da un timer, ed e' solitamente maggiore di 100; di conseguenza Kb deve essere un numero piuttosto grande, intorno al 1000. Tra l'altro ci tengo a farvi notare che c0=Kb, essendo k0=1.
Detto questo la domanda e': "Che formato scegliamo per Kb e
kn?"
Per semplificare al massimo ho scelto un formato in virgola fissa
16.16 bit per rappresentare qualsiasi valore. Nel caso specifico la
cosa risulta ulteriormente semplificata: Kb viene troncato
alla sola parte intera e rappresentato con 16 bit senza segno; di
kn viene tenuta la sola parte decimale, anche questa
rappresentata con soli 16 bit. Il risultato e' un valore 16.0 bit
moltiplicato per un valore 0.16 bit che da un risultato 16.16 bit.
In realta' essendo questo il valore di cn si potrebbe evitare
di calcolare la parte decimale, che andrebbe comunque troncata.
Questo metodo non ricorsivo sembra non soffrire della propagazione degli errori che sarebbe invece presente nel metodo ricorsivo: nel nostro caso l'errore dato dall'approssimazione affligge il singolo cn non estendendosi a tutti quelli successivi.
Il risultato di questo metodo di calcolo e' visibile nel grafico qui sotto.
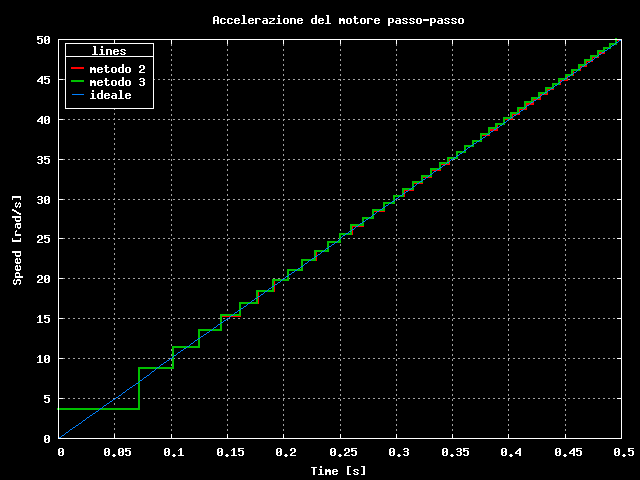
Confronto tra virgola mobile e virgola fissa
Come si vede il calcolo con virgola fissa ricalca abbastanza
fedelmente il risultato ottenuto in virgola mobile.
Parafrasando il grande genio direi: "88 miglia all'ora!!!"
Un piccolo appunto sulla moltiplicazione di valori in virgola fissa: Kb viene rappresentato con la sola parte intera, e' quindi in un formato 16.0 bit; di kn viene invece tenuta la sola parte decimale, il suo formato e' 0.16 bit. In entrambi i casi abbiamo due valori a 16 bit senza segno che vengono moltiplicati tra loro. La moltiplicazione pura tra interi senza segno produce un risultato a 32 bit che nel nostro caso risulta gia' nel formato corretto 16.16 bit; quindi basta troncare la parte decimale per avere cn in formato intero a 16 bit.
Piccoli spostamenti
Fin qui e' andato tutto bene: abbiamo messo insieme il metodo per accelerare regolarmente, raggiungere la nostra velocita' di crociera e poi rallentare fino ad essere completamente fermi, il tutto seguendo il nostro profilo impostato. Ma nel caso di piccoli spostamenti dobbiamo stare a fare tutta questa tiritera?
A questo punto le masse si dividono tra due scuole di pensiero, quelli che dicono: "Si, certo, bisogna sempre seguire il profilo di accelerazione" e quelli disposti ad ammettere che in fin dei conti per fare pochi passi forse non e' il caso di stare a scomodare tutto questo casino, una frequenza fissa alla fine puo' bastare.
Riflettiamo un attimo osservando di nuovo il primo grafico di questa pagina:

Grafico velocita'-coppia
All'inizio abbiamo detto che a velocita' inferiori alla max starting speed il motore si avvia sempre, a meno che il carico non sia eccessivo per la velocita' scelta. Questo significa che a patto di scegliere comunque una velocita' opportuna, possiamo muoverci a velocita' costante; inoltre cosi' come siamo partiti da fermi senza problemi possiamo fermarci all'istante.
Queste considerazioni ci permettono di coniare una nuova regola: se lo spostamento e' contenuto (meno di una quarantina di passi) sarebbe uno spreco tentare di accelerare per il gusto di rallentare immediatamente, possiamo quindi muoverci a velocita' costante per tutto il tratto, velocita' che rimane comunque confinata nella start region.
Questo ci fa introdurre un nuovo concetto: la frequenza minima degli impulsi e il nuovo coefficiente Kc:
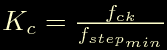
In caso di moto accelerato applichiamo la regola vista sopra:

mentre in caso di moto uniforme applichiamo la piu' semplice regola:
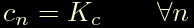
Se osserviamo i grafici sopra che riportano la proggressione dei
passi noteremo come i primi passi (in particolare il primo) siano
molto larghi, di fatto il motore alla partenza e all'arrivo
sgrana producendo un rumore piuttosto fastidioso.
Abbiamo appena detto che possiamo muoverci a velocita' costante ad
una particolare frequenza, allora perche' non fondere le due cose?
Possiamo calcolare la sequenza dei coefficienti cn utilizzando
Kb, come se stessimo accelerando, ma nel caso in cui questo
valore fosse superiore a Kc possiamo restringere a questo il
valore calcolato. Questa tecnica equivale a dire che abbiamo una
velocita' minima (o una frequenza minima degli impulsi) da garantire
al di sotto della quale non e' possibile andare.
Il nostro profilo di velocita' sarebbe modificato in questo modo:
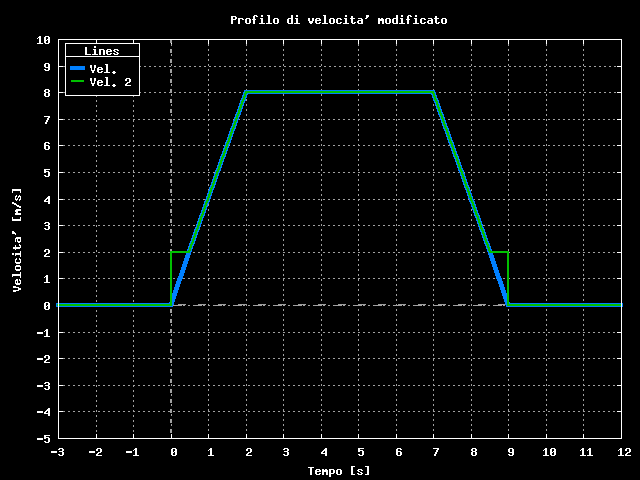
Profilo di velocita'
Implementazione
Tutto quanto descritto fin qui e' stato da me implementato a bordo di un ATmega128, qualcuno non sara' contento della scelta ma io sono ancora innamorato di questa famiglia di microcontrollori. Ovviamente il tutto sviluppato interamente in assembler, mi sembra ovvio.

Demo kit
L'aspetto non e' dei migliori ma lo sviluppo del software e' ancora in corso, l'hardware segue di conseguenza come puo'; al momento il controllo e' quasi esclusivamente tramite terminale seriale. La versione attuale e' scaricabile dalla sezione download.
Visto che un'immagine vale piu' di mille parole, vediamo il segnale generato: questo e' un esempio che mostra l'accelerazione fino alla velocita' impostata, il movimento a velocita' costante e quindi la decelrazione. Per ottenere tutto il ciclo in pochi passi, questi sono 30 passi totali, ho dovuto taroccare un pochino i parametri.
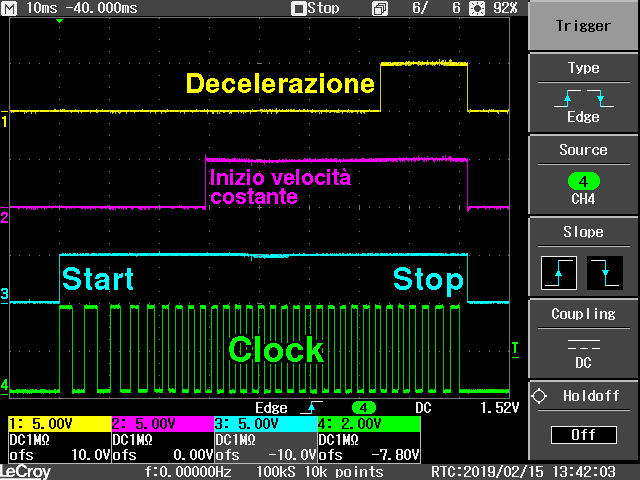
Clock signal
Qui sotto il dettaglio del primo impulso generato.
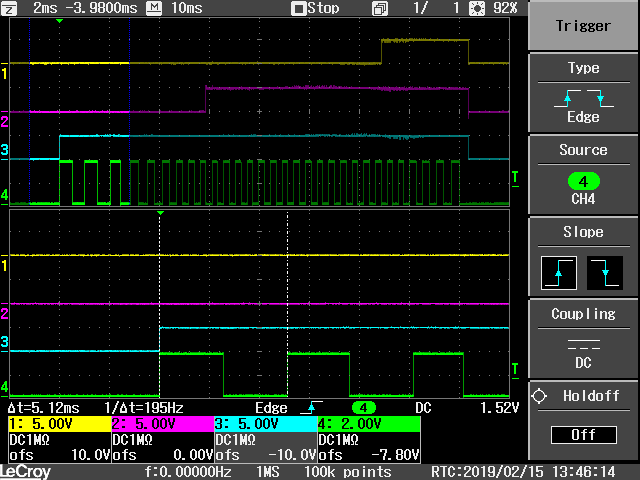
Clock signal
Per facilitare il debug ho collegato un pin all'esecuzione dell'interrupt handler: in questo modo e' possibile cronometrare il tempo di esecuzione della routine di gestione dell'interrupt.
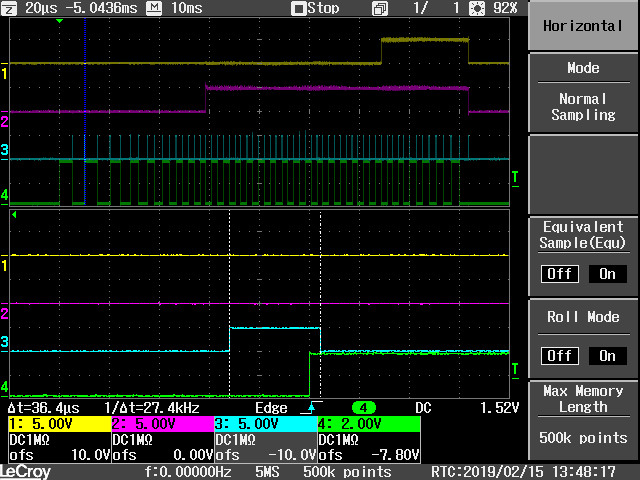
Interrupt handler execution time
Impostando la permanenza ad infinito possiamo catalogare tutte le durate dell'interrupt handler: l'esecuzione e' molto veloce in corrispondenza della discesa del segnale di clock. Il momento in cui il clock va sollevato e' sicuramente piu' impegnativo: l'interrupt handler gestisce 3 assi e non tutti fanno il passo insieme, quindi non tutti i clock vanno alti contemporaneamente; l'esecuzione dell'interrupt handler puo' raggiungere i 42us.
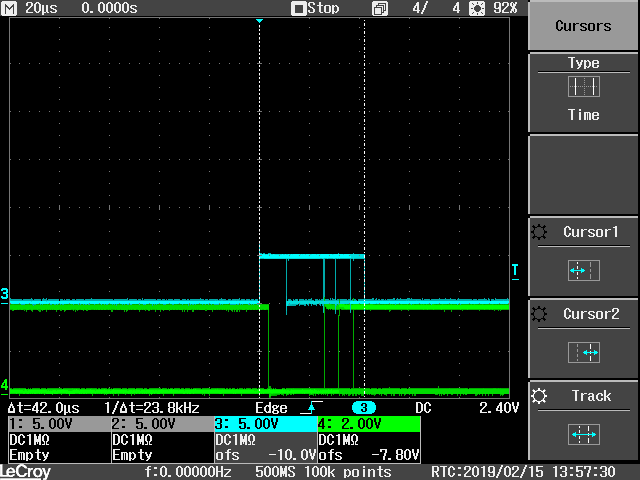
Interrupt handler execution time
Approssimando a 50us e moltiplicando per 2 si ottiene un periodo di 100us, il cui inverso vale 10kHz. Questo vuol dire che l'interrupt handler dell'orologio potrebbe generare comodamente frequenze fino a 10kHz, ben oltre quello che ci serve per pilotare i passo-passo.
Variazione dinamica
Ora che tutto funziona per il meglio vogliamo complicare ulteriormente il gioco: supponiamo di avere un movimento molto lungo, molti passi per una durata complessiva di decine di secondi se non addirittura minuti. Sarebbe possibile variare la velocita' del motore dinamicamente una volta che e' in movimento?
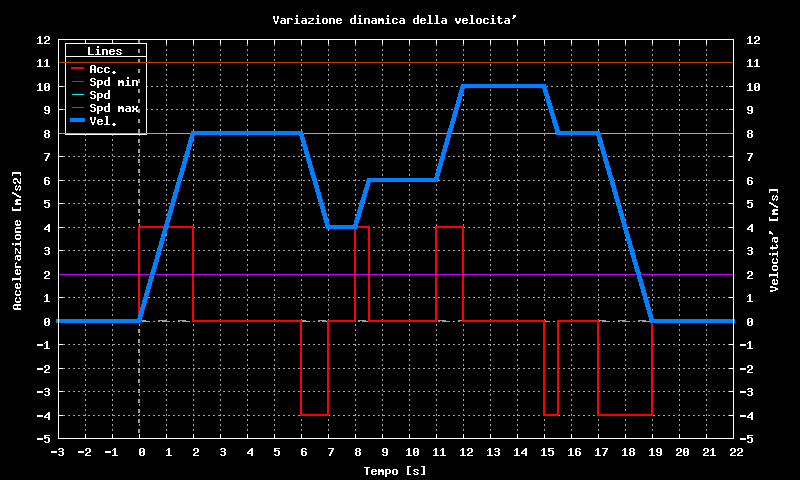
Variazione dinamica durante il movimento
Cerchiamo di capire quali sono le regole del gioco: il numero totale di passi e' stato stabilito e a meno di problemi gravi durante il percorso non ci saranno ripensamenti. L'accelerazione dipende dal sistema ed e' stata tarata, quindi non e' in discussione. Qualcuno potrebbe suggerire che comunque un'accelerazione inferiore a quella stabilita sarebbe comunque lecita; vero, ma per il momento soprassediamo. L'unica cosa che chiediamo e' di poter variare la velocita' con cui l'asse (o gli assi) si muoverebbe, ad esempio perche' sul cammino ci sono dei passaggi critici o delicati.
L'unico esempio che mi viene in mente in questo momento e' quello
della bobinatrice. Supponete di pilotare il motore di una
bobinatrice, avete scelto un passo-passo perche' vi permette di
contare asattamente le spire, inoltre non avevate in casa nient'altro
e i negozi avevano chiuso tutti per ferie fino a data da destinarsi.
Quindi stabilite il totale dei passi, quindi delle spire che volete
avvolgere; abbassate un pochino l'accelerazione in modo tale che
parta dolcemente e scegliete una buona velocita' per il lavoro.
Malgrado le migliori intenzioni del mondo mentre la bobinatrice
avvolge non sarebbe confortevole poter variare la velocita'?
Sia in piu' che in meno. Magari avete scelto una velocita' di
crociera troppo bassa; in fin dei conti se fosse stato un motore DC
avreste sicuramente messo una bella manopola per controllare la
velocita', no!!?!!
La risposta all'interrogativo sembra essere si. Al momento (versione 0.07) la variazione dinamica della velocita' non e' implementata, sicuramente in qualche versione futura.
BL-TB6560-V2.0
Vediamo ora alcuni driver di potenza. Una scheda abbastanza diffusa in questo periodo e che si riesce a reperire ad un prezzo conveniente, e' la BL-TB6560-V2.0 basata sul driver TB6560. A prima vista sembra una scheda molto bella: completamente optoisolata, tutte le regolazioni su dip switch, tabelle stampate direttamente sul pcb e sempre a portata di mano, pochi collegamenti, alimentabile fino a 24V, in grado di gestire il microstepping fino a 1/16 di passo. In realta', guardando meglio, sembra veramente una ciofeca!

Scheda BL-TB6560-V2.0
Non sono stato in grado di trovare lo schema elettrico (ufficiale o meno) di questa maledetta scheda, cosi' mi sono messo a fare un po' di sano reverse engineering e sono emerse delle cose piuttosto impressionanti.
Una delle prime cose che mi aveva colpito fin dalle prime prove era il fatto che pur non alimentando l'ingresso EN il motore girasse ugualmente. Al momento non gli diedi molta importanza, ma la cosa ancora piu' sconvolgente fu scoprire che con l'ingresso EN alimentato il motore non girava piu'. Io non saro' un genio, ma mi sembra che il concetto di contatto di sicurezza sia stato un po' travisato dal progettista mascherato (in questa pagina ho battezzato progettista mascherato il padre di questa scheda, chiunque esso sia).
L'immagine qui sotto mostra il collegamento degli ingressi optoisolati, effettivamente il segnale ENABLE, che deve essere alto per abilitare le uscite, e' attivo fin tanto che l'ingresso EN non viene alimentato, mentre inibisce le uscite di potenza se alimentato.
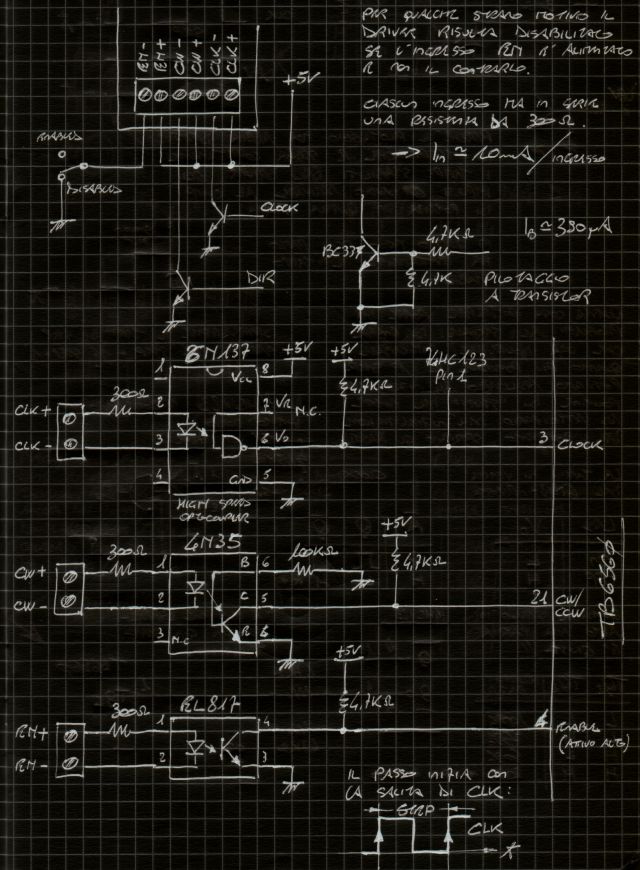
Collegamento degli ingressi
Questo non e' l'ultimo dei mali, dopo tutto la sicurezza si puo' ottenere anche tagliando direttamente l'alimentazione a 24V, anche il segnale CLK gode della stessa bizzarra inversione. Mentre per l'ingresso EN non si puo' fare niente: se il led e' alimentato l'uscita e' disabilitata, non ci sono santi, questa volta si puo' tentare un escamotage.
Con questo trucco possiamo fare in modo che il segnale CLK sul pin 3 del TB6560 ricopi senza alcuna inversione il segnale pilota prodotto dal nostro controller.
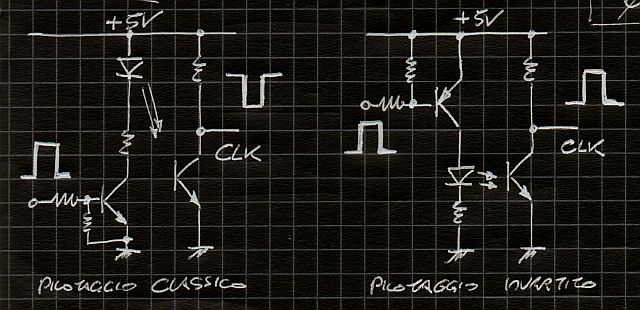
Pilotaggio dell'ingresso CLK
Sulla sinistra il circuito che chiunque sarebbe portato ad utilizzare, sulla destra invece lo stesso circuito opportunamente modificato per non invertire il segnale CLK.
Il segnale CLK presente sul pin 3 del driver viene riportato anche all'ingresso di un 74HC123; questo e' un prolungatore di impulso che modifica la corrente negli avvolgimenti durante la marcia del motore. L'intento e' quantomeno lodevole: uno dei problemi (tra i tanti) che si ha nel controllare i motori passo-passo consiste nella corrente di stazionamento. Se durante la rotazione negli avvolgimenti del motore scorrono 3A perche' il nostro motore e' di dimensioni ragguardevoli, questo non vuol dire che il motore necessiti di 3A anche per stare fermo; a lungo andare questa corrente non fara' altro che scaldare il nostro povero motore. Il trucco consiste nel ridurre o nell'azzerare la corrente di stazionamento del motore: tanto se non deve girare e' inutile che consumi.
Il 74HC123 serve ad implementare un meccanismo completamente automatico e trasparente all'utente che mantenga la corrente impostata durante la marcia, ma riduca la corrente negli avvolgimenti una volta che il motore viene giudicato fermo. Il principio e' semplice: il 74HC123 allunga gli impulsi di clock, riavviando il conteggio ad ogni nuovo impulso di clock e quindi garantendo che la corrente negli avvolgimenti decresca solo dopo un certo intervallo di tempo dall'ultimo impulso ricevuto.
Purtroppo anche qui il progettista mascherato ci ha messo lo zampino: il TB6560 inizia il passo con la salita del segnale CLK, ma il 74HC123 inizia a contare dalla discesa di CLK; il risultato: per meta' del primo passo il motore si muove a corrente limitata.
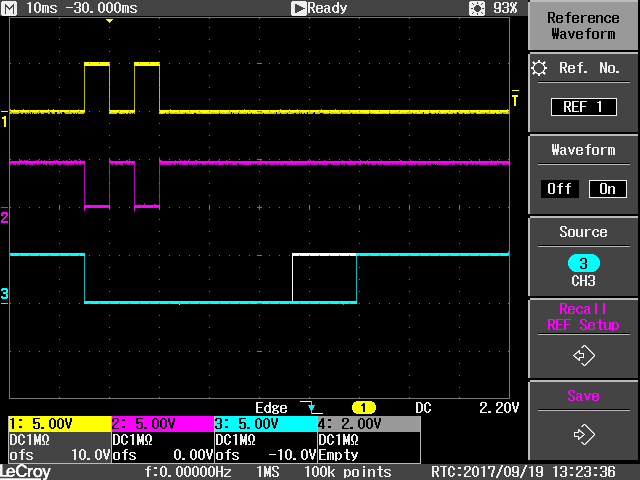
Vista degli impulsi di controllo
Qui sopra ho catturato il singolo passo: in giallo il segnale pilota prodotto dal controller, in viola il segnale CLK che arriva sul pin 3 del TB6560, e' invertito perche' l'ingresso e' collegato tramite il circuito classico visto prima. La traccia azzurra e' l'uscita del 74HC123: la corrente si alza quando il segnale va basso.
La modifica
Vediamo come e' possibile modificare la scheda BL-TB6560-V2.0 in modo da ridurre i difetti di cui sopra.
Prima di tutto rimuoviamo: U6, R16 ed R18. Visto che il 74HC123 non e' affidabile per il controllo della corrente degli avvolgimenti, tanto vale toglierlo di mezzo; alla fine avremo un controllo manuale della corrente di stazionamento.

Rimozione di: U6, R16 ed R18
Tagliamo la pista al di sotto del dip-switch.

Taglio della pista
Tagliamo la pista che passa per C2 e la colleghiamo diretamente a +5V.

Collegamento a +5V
Saldiamo un diodo 1N4148 tra il pin tagliato di S1 ed un capo di R18

Inserimento del diodo 1N4148
DRV8825
Anche questa e' una schedina molto famosa, probabilmente deve molto della sua fama alle stampanti 3D, per fortuna questa volta ho trovato uno schema elettrico originale che mi ha ridotto notevolmente il lavoro.

Scheda DRV8825
Si tratta di un driver della Texas montato su un pezzetto di pcb veramente minimale che espone il minor numero possibile di pin. Anche in questo caso il Progettista Mascherato ha colpito ed ha lasciato il segno.
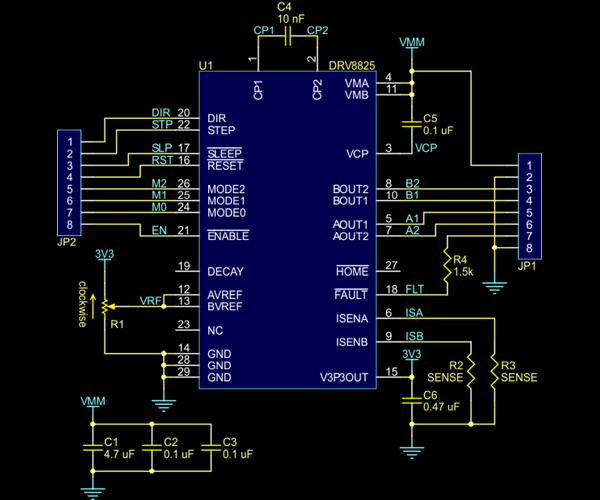
Schema elettrico DRV8825
In linea di principio la piccola schedina semplifica i collegamenti del driver lasciando solo cio' che serve veramente, peccato che poi serva una matriosca di schede e adattatori per arrivare dalla CPU fino al motore. La piccola schedina ha un solo elemanto di calibrazione, c'e' sopra un trimmer, con un po' di fantasia qualcuno avra' sicuramente gia' sentenziato che serve a regolare la corrente degli avvolgimenti, inffatti e' proprio cosi': regolando l'unico trimmer presente si regola la corrente che scorre negli avvolgimenti del motore. Buttiamo un occhio al data sheet del DRV8825, al suo interno troveremo la seguente frormula per il calcolo della corrente di chopping:
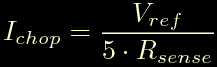
Ovviamente il trimmer regola Vref da 0 a 3.3V, come si vede dallo schema elettrico; nel circuito sono montate delle Rsense da 0.1 ohm; tutto questo porta ad una corrente negli avvolgimenti di soli:
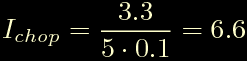
6.6A!!! Ma non saranno un po' troppi?!?! Il driver arriva solo a 2.5A.
Al solito hanno dimenticato un componente marginale ma importantissimo: una resistenza in serie al ramo principale del trimmer per fare in modo che non arrivi fino a 3.3V; tra l'altro la presenza di un piccola resistenza di limitazione mi avrebbe permesso di calibrare questi driver in modo piu' agevole e preciso, per ora basta ricordarsi di non superare mai gli 1.25V; la tensioni di riferimento e' misurabile mettendo i puntali del tester sui piedini del trimmer.
Per collaudare questi driver e poter fare qualche prova ho messo insieme una piccola basetta con un paio di motori recuperati da vecchi harddisk, per quanto possa sembrare banale il dispositivo mi ha dato non poco filo da torcere: i motori avevano un comportamento molto nervoso e per quanto io li pilotassi sempre nella stessa direzione continuavano ad andare avanti e indietro. Per pochi passi sembravano fare il movimento corretto, ma appena credevo di aver risolto il problema riprendevano a muoversi a casaccio avanti e indietro.
Ci ho messo un po' a capire che la corrente di pilotaggio era troppo elevata! Per pilotare correttamente questi motori e' necessario impostare la Vref intorno ai 40mV, secondo la formula sopra questo dovrebbe produrre una corrente di 80mA per avvolgimento.

Collaudo driver
Regolazione della corrente nel DRV8825
Come al solito sembrava un'operazione banale, almeno fino a che non mi ci sono messo sul serio: la regolazione della corrente negli avvolgimenti richiede una certa attenzione.
Come mostra il data sheet, la corrente che scorre nel singolo avvolgimento e' la stessa che scorre nella resistenza di sensing. Sembra una cosa banale, ma vale la pena puntualizzare: questa cosa tornera' fuori in modo pesante piu' avanti, quando calcoleremo la potenza dissipata dalla stessa Rsense.
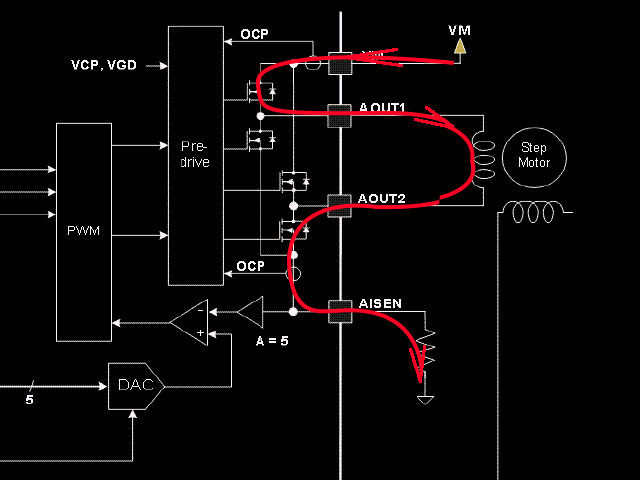
DRV8825 data sheet
Il data sheet riporta la seguente relazione per la corrente di chopping:
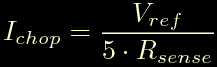
Ci sono due limiti che vanno sempre rispettati:
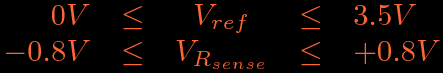
La prima e' abbastanza facile da rispettare, la seconda serve per non sfondare l'ingresso analogico. Ora essendo
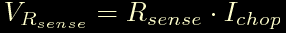
Sostituendo Ichop si ottiene:
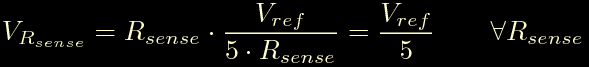
quindi VRsense e' sempre un quinto di Vref. Per avere un margine di sicurezza poniamo VRsense max pari a 0.6V, questo implica un limite di 3.0V per Vref.
Ora possiamo mettere tutte queste informazioni in un bel grafico Ichop - Vref.
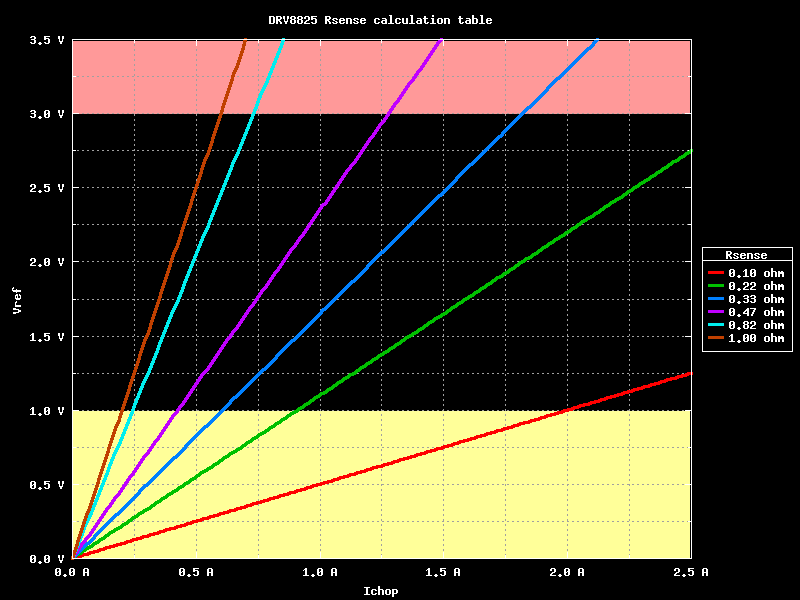
Calcolo Rsense
Nel grafico sono evidenziate due zone: la prima per Vref > 3.0V, come detto sopra questo corrisponde ad una caduta su Vref > 0.6V. La seconda per Vref minore di 1.0V, quest'area e' indicata nel data sheet per avere una risoluzione inferiore nel determinare la Vref finale.
Il nostro progettista mascherato ha scelto delle Rsense da 0.1 ohm, spingendoci al limite della zona gialla; la curva e' molto comoda per correnti elevate, ma diventa piuttosto scomoda se serve di abbassare la corrente.
Non bisogna trascurare gli effetti termici: purtroppo o per fortuna la nostra Rsense sono percorse dalla stessa corrente che circola nelgi avvolgimenti, che lo vogliamo no queste dissiperanno potenza per effetto Joule. La cosa e' ancora piu' sensibile se si vuole miniaturizzare tutto il driver. La tabella per il calcolo della potenza puo' aiutarci nella selta del case del componente, ancora maglio possiamo riportare delle curve iso-potenza sul grafico precedente che mettano in evidenza la dimensione del componente necessaria per Rsense.
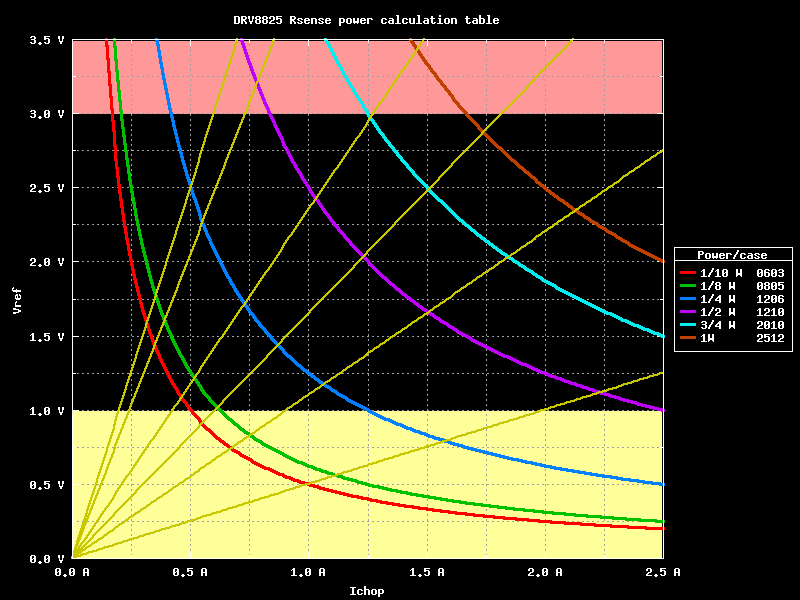
Rsense power
Come si vede la dimensione fisica di Rsense cresce abbastanza velocemente. Un'idea di massima potrebbe essere quella di adottare un case 1201 in grado di dissipare fino a 1/2 W, dopodiche' scegliere una Rsense da 0.10 ohm per le alte correnti e 0.82 ohm per le basse; in questo modo si evita di entrare nell'angolo in alto a destra al di sopra della curva viola.
Download
Se qualcuno fosse interessato agli script per la generazione dei grafici e delle formule matematiche viste sopra, trova tutto qui.
| step_equ | Script per la generazione delle formule matematiche, richiede LaTeX e l2p. |
| step_equ2.sh | |
| step_equ3.sh | |
| step_grp2.tar.gz | |
| step_grp3.tar.gz | |
| ramping-0.01.tar.gz | Codice per la generazione delle tabelle e dei grafici di accelerazione, puo' generare il movimento completo del motore. |
| ramping-0.02.tar.gz | Codice per la generazione dei grafici aggiuntivi e dei regoli stampabili per il calcolo e la verifica delle velocita' e delle accelerazioni. |
| stepctrl-0.07.tar.gz | Firmware per ATmega128, versione provvisoria, il controllo avviene quasi esclusivemente da seriale. |
| stepctrl-0.12.tar.gz | Prima versione decente, contiene un prototipo di foratrice automatica. |