Da non fare mai
Facciamo una piccolissima introduzione prima di tutto: consideriamo il sistema di controllo generico rappresentato in figura:
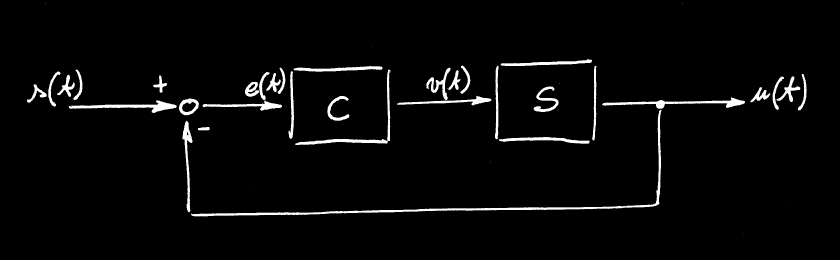
Sia S il sistema da controllare, u(t) e' l'uscita del sistema S, la grandezza che vogliamo controllare, v(t) e' l'ingresso del sistema controllato, ed e' anche l'uscita prodotta dal nostro controllore C; per finire s(t) e' il setpoint e e(t) e' l'errore che entra nel nostro controllore. Ovviamente quello che vogliamo e' avere u(t) il piu' possibile uguale a s(t).
Visto che si parla di PID vorremo realizzare il controllore C tramite una caratteristica proporzionale, integrale, derivativa. La figura qui sotto mostra l'interno di un controllore PID analogico, le costanti Kp, Ki e Kd determinano il comportamento del controllore.
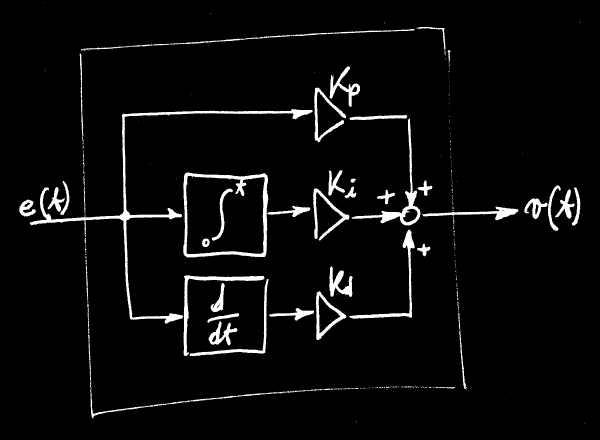
Volendo realizzare il controllore in modo digitale bastera' quindi trasformare questo semplice schemino in una espressione digitale, quindi possiamo scrivere:
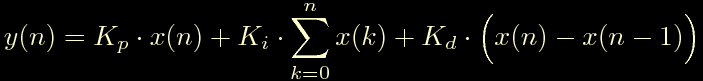
Questa formula e' quanto di piu' sbagliato possiate realizzare. Questa cosa va sempre evitata, non funziona minimamente ed e' intrinsecamente instabile!
Implementazione corretta
L'implementazione corretta di un controllore PID digitale e' questa:
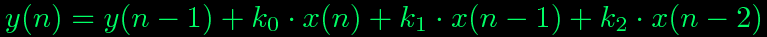
Capisco che la cosa possa cogliervi un po' di sorpresa, ma vi posso garantire per esperienza personale che e' cosi. Qualcuno avra' gia' intuito che una formula di questo tipo puo' rappresentare qualunque cosa, il vero segreto sta nei coefficienti. Per chi fosse anche solo vagamente curioso cerchero' di giustificare la provenienza di questa espressione, chi non ha pazienza puo' saltare il capitolo e passare direttamente a "Che cos'e' quella cosa?!?!!".
Perche' quella cosa
Cerchiamo di capire da dove arriva l'espressione vista sopra, per fare questo ripartiamo dal PID analogico visto prima, per semplicita' riporto qui sotto lo schema a blocchi.

La funzione di trasferimento del controllore puo' essere scritta come:
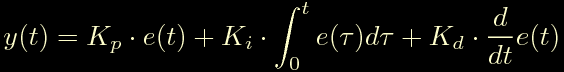
Ora in questa raccogliamo Kp e la riscriviamo in questo modo:
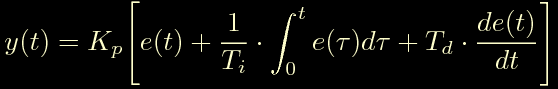
In questa forma il coefficiente Ti esprime il tempo in secondi in cui vogliamo che l'integrale azzeri l'errore, mentre il coefficiente Td esprime di quanti secondi la predizione della derivata e' proiettata nel futuro. Visto che ci stiamo ancora muovendo nel tempo continuo, dobbiamo passare al tempo discreto, cioe' alla trasformata z. Per far questo cerchiamo di ricordarci come si fa a derivare e integrare nel dominio della trasformata z.
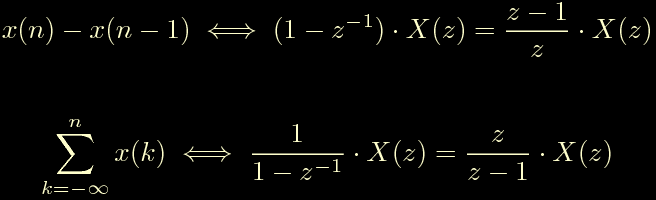
La prima riga ci ricorda che derivare nel tempo discreto equivale a moltiplicare per 1-z^-1 nel dominio della trasformata z, la seconda riga ci ricorda che integrare nel tempo equivale a moltiplicare per l'inverso di 1-z^-1. Ora sostituiamo all'interno dell'espressione sopra e otteniamo la trasformata z del controllore PID. Visto che otteniamo la trasformata z siamo gia' nel tempo discreto.
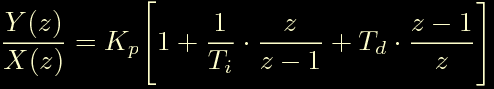
Capisco che sia un po' cruda da digerire in un primo momento.
E' importante ora fare una
precisazione: siamo nel tempo discreto, quindi Ti e Td
che sono misurate in secondi non sono piu' adatte al nostro mondo, le
sostituiamo ripettivamente con Si ed Sd che invece sono
misurate in campioni (samples).
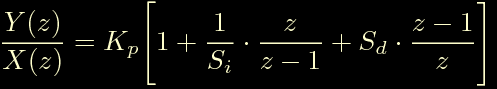
Per mantenere un minimo di rigorosita' vi ricordo che:

In cui Dt (delta t) e' semplicemente l'intervallo di campionamento del tempo discreto; in questo modo il passaggio dal tempo reale, in cui e' comodo fare i conti e il tempo discreto in cui si muove vermante il nostro PID e' sato ufficializzato.
Ora non ci resta che fare i conti.
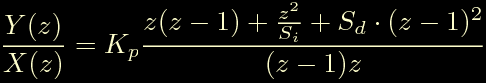
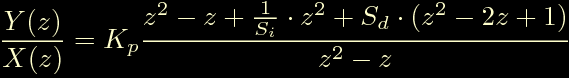
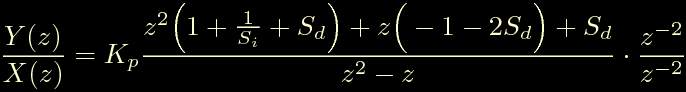
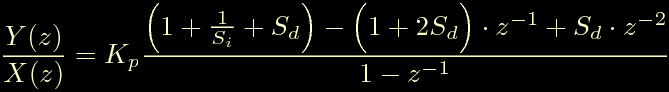
Ora procediamo come al solito portando a destra il termine X(z) e a sinistra il termine 1-z^-1, otteniamo la forma:
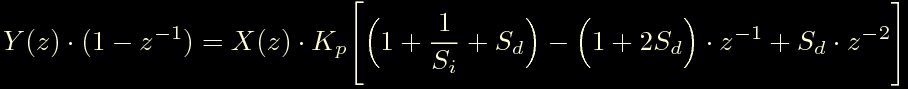
Che si traduce nell'equazione alle differenze finite:
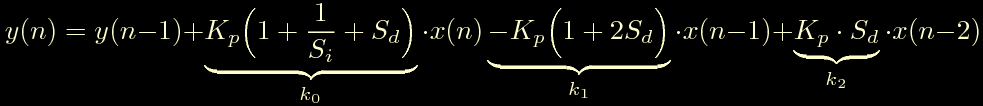
Che e' proprio l'equazione che volevamo ottenere.
La riporto qui sotto per semplicita'.
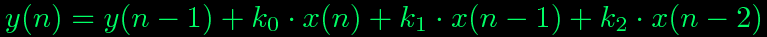
Cos'e' quella cosa?!?!!
Cerchiamo di capire che cosa abbiamo davanti, tanto per incominciare la riscriviamo in questo modo:
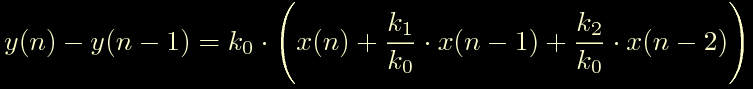
Sulla sinistra abbiamo un polo in 1, sulla destra abbiamo un guadagno k0 e un filtro FIR tra parentesi. In funzione dei coefficienti che mettiamo nella parte di destra possiamo trasformare questo filtro in qualunque cosa, ma secondo il mio modestissimo parere questo coso ha senso solo se ha due zeri complessi coniugati.
Perche' il filtro di destra abbia due zeri complessi coniugati devono valere le seguenti relazioni:

Per chi amasse il piano complesso z ecco la posizione dei poli e degli zeri: un polo fisso in 1 e due zeri complessi coniugati che potenzialmente potrebbero trovarsi ovunque nel piano complesso.
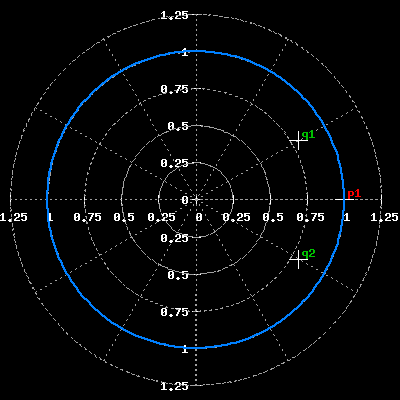
Calcolo delle costanti
Veniamo ora al nocciolo della questione: in qualche modo ci siamo rassegnati al fatto che un controllore PID si realizzi in questo modo:
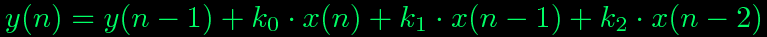
Quello che non e' ancora chiaro e' come si calcolano i coefficienti: k0, k1, k2. Vi confesso che su questo ci sono ancora delle contese aperte da diversi anni, ma non vi spaventate, procediamo con calma.
Prima di tutto seguiamo quanto scritto fin qui visto che gode di un certo rigore matematico, riprendiamo quanto scritto sopra e mettiamo in evidenza i nostri coefficienti.
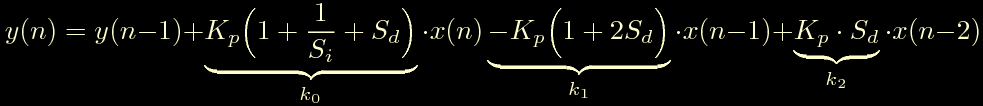
Estraiamo i coefficienti k0, k1, k2 e mettiamoli in una bella tabella riassuntiva.
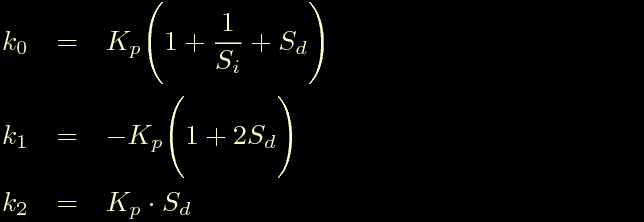
Questo e' valido se vogliamo esprimere i coefficienti del controllore in funzione dei parametri S che misurano i tempi integrale e derivativo in campioni, se volessimo esprimerli in secondi basterebbe sostituire le espressioni di Si ed Sd riportate sopra ed ottenere la seguente tabella.
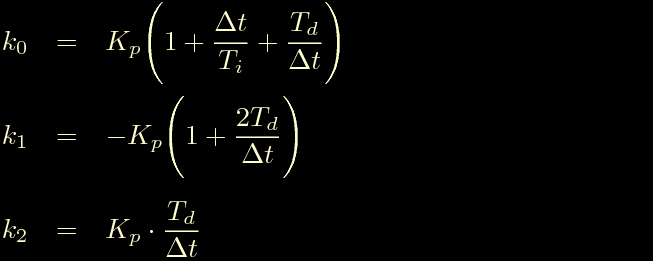
La favola potrebbe concludersi qui, abbiamo tutto quello che ci serve: una equazione alle differenze finite che funziona e una bella tabella per calcolarne i coefficienti, il PID e' servito.
Io invece mi dilunghero' ancora un pochino, perche' sono curioso di vedere come si muovono sul piano complesso i due zeri complessi coniugati, chi fosse interessato mi segua.
Come si muovono gli zeri cc
Riprendiamo per un istante la forma con Si e Sd:
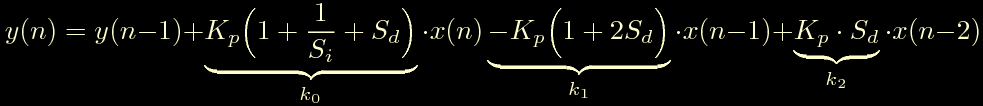
Notiamo che in questa forma Sd si puo' azzerare, questo equivale ad escludere completamente l'azione derivativa del controllore, mentre Si non puo' mai azzerarsi, anzi, piu' Si si avvicina a zero e piu' l'azione integrale ne risulta esaltata, per escludere l'azione integrale Si dovrebbe tendere ad infinito. Non credo di averlo ancora indicato esplicitamente, ma e' sottinteso che Si e Sd siano sempre positivi.
Annullando Sd escludiamo la derivata ed otteniamo la seguente forma per il nostro controllore PI:
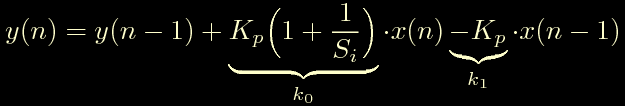
Il polo e' rimasto in 1 e da li non lo schioda nessuno, invece gli zeri complessi coniugati sono diventati un solo zero reale che si trova in:
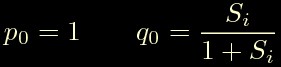
Come abbiamo gia' visto prima per Si che tende a zero, lo zero q0 tende a zero e di conseguenza l'azione integrale del controllore tende a divergere: abbiamo un polo in 1 e uno zero che si sposta verso 0, che quindi tende a sparire lasciando completamente scoperto il polo. Viceversa per Si che tende ad infinito q0 tende a 1, riducendo l'azione integrale del controllore: tende a cancellare l'unico polo dell'equazione.
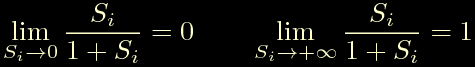
Direi quindi che piu' lo zero si avvicina a 1 e piu' inibisce l'azione integrale del controllore, piu' si allontana da 1 e piu' la esalta.
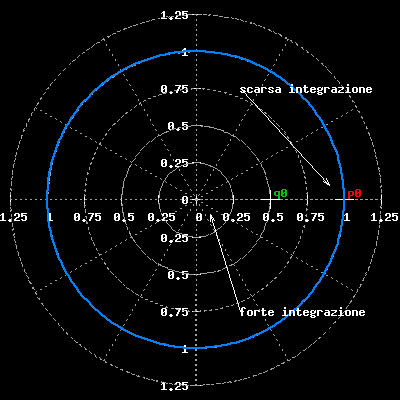
Per chi preferisce i diagrammi di Bode ecco l'andamento in frequenza in anello aperto:
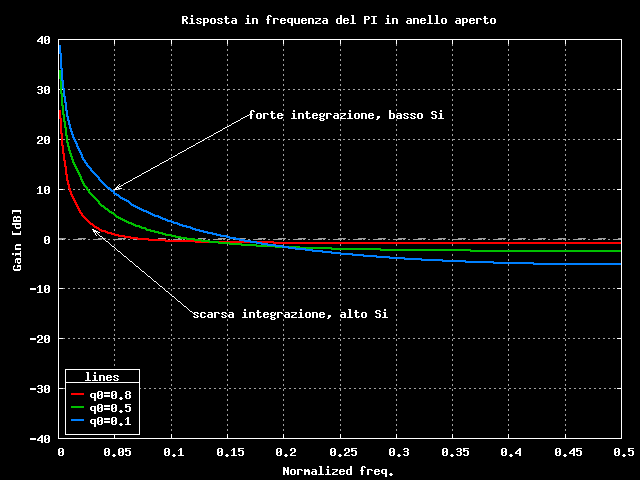
Bene, ora complichiamo un po' le cose tornando al PID completo, dalla discussione sui filtri digitali sappiamo che la formula generale di un filtro che abbia un polo reale e due zeri complessi coniugati e' la seguente:
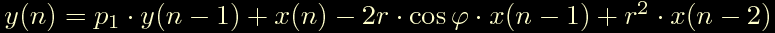
Se osserviamo l'equazione del nostro PID:
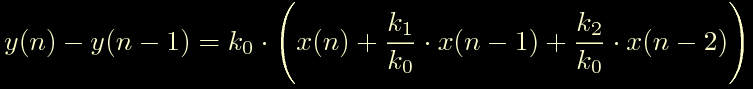
troviamo la relazione gia' vista prima:

non ci resta che sostituire le definizioni di: k0, k1, k2, per vedere dove andiamo a cascare:
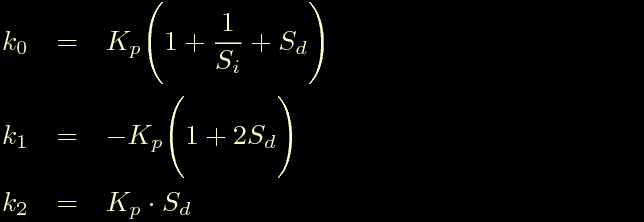
Cominciamo con r perche' sembra piu' semplice:
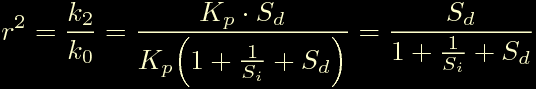
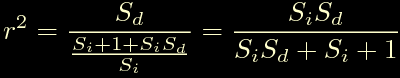
Da cui si ottiene:
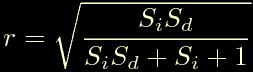
Ora facciamo lo stesso per cos(fi), partiamo scrivendo:
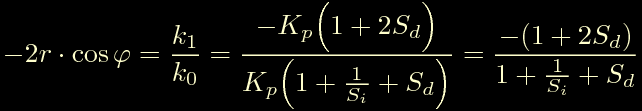
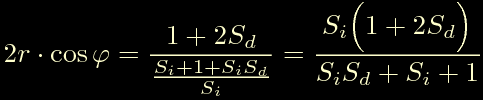
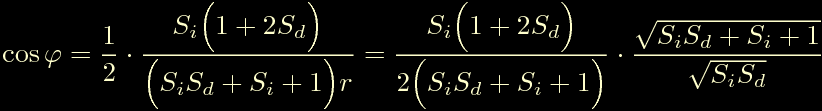
Otteniamo infine:
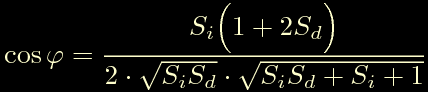
Per maggiore chiarezza raduniamole entrambe:
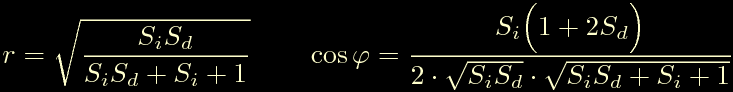
Queste sono le coordinate polari degli zeri complessi coniugati in funzione dei parametri Si ed Sd.
La seconda ci impone di essere piu' restrittivi con Sd che ora non puo' piu' azzerarsi:

Nasce inoltre una nuova restrizione, la terza qui sopra: perche' il coseno abbia un senso deve essere al limite Si = 4*Sd, se fosse Si > 4*Sd allora risulterebbe cos(fi) > 1, da cui sarebbe un problema ricavare fi.
Veniamo ora al momento tanto atteso: quelle riportate qui sopra sono
le coordinate polari degli zeri complessi coniugati del nostro
PID, come si muovono nel piano?
Ecco il luogo degli zeri in funzione di Si ed Sd:
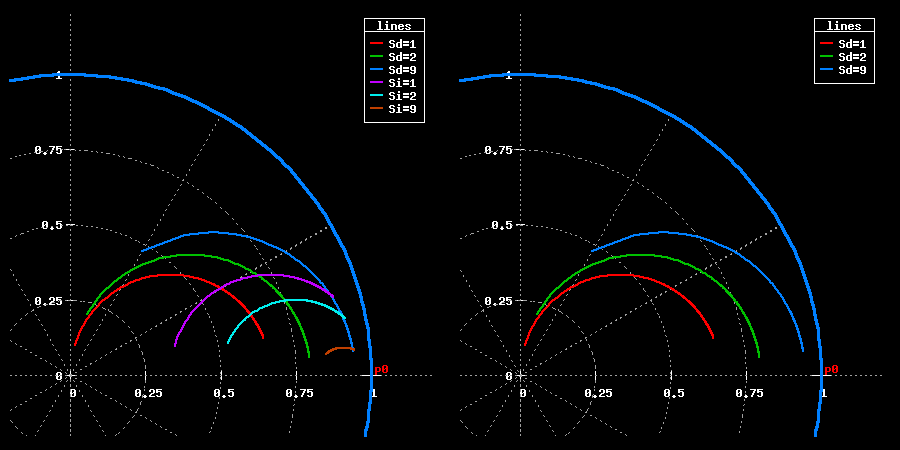
Sulla sinsitra ho riportato entrambe le famiglie di curve: per Sd costante e per Si costante, per maggiore pulizia del grafico sulla destra ho riportato le sole famiglie di curve per Sd costante. Al crescere di Si l'azione integrale del PID e' sempre meno pronunciata, infatti gli zeri si avvicinano sempre piu' al polo in 1. All'aumentare di Sd aumenta l'azione derivativa del PID, strano che questo avvicini sempre piu' gli zeri al polo in 1.
Al momento non riesco a dare una interpretazione chiara della cosa, per il momento lo prendero' come un dogma della fede.
Vediamo comunque di associare a queste curve il corrispondente comportamento in frequenza del PID, ovviamente in anello aperto:
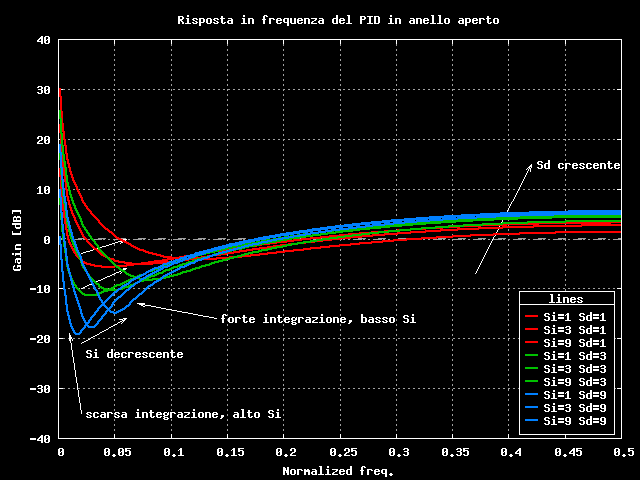
Esaltando sempre piu' l'effetto derivativo del PID la curva si schiaccia alle basse frequenze, ma si solleva sempre di piu' alle alte frequenze.
Due scuole di pensiero
Ancora una volta il discorso potrebbe essere finito qui, questa volta ci siamo detti veramente tutto, ma io mi dilunghero' ancora per un'ultimo capitolo facendo ancora qualche elugubrazione sul PID. Per molti anni ho calcolato i coefficienti dell'equazione alle differenze finite in modo completamente diverso e per tutti questi anni ho avuto la sensazione di essere preso in giro dai miei stessi controllori, ora e' giunto il momento di fare chiarezza.
Correva l'anno Domini 2001, o giu' di li, e in ditta stavo affrontando il controllo di velocita' di un motore industriale in corrente continua, il motore doveva girare molto lentamente e il mio controllo di velocita' non aveva nessuna voglia di funzionare; non c'era verso di mantenere la rotazione del motore a bassi regimi. Un collega mi passa un numero di Progetto elektor dell'epoca, in cui veniva affrontato proprio un problema simile: sulla rivista il controllo di velocita' avveniva attraverso un PID digitale. Senza capire fino in fondo quello che stavo facendo copiai le formule per il calcolo dei coefficienti, copiai l'equazione alle differenze finite e inserii il tutto nel mio codice: magicamente il mio anello di velocita' prese a funzionare. Dopo una sistemata ai parametri riusciva a muovere il motore lentissimamente mantenendo costante la velocita' nel tempo. I coefficienti erano calcolati in questo modo:
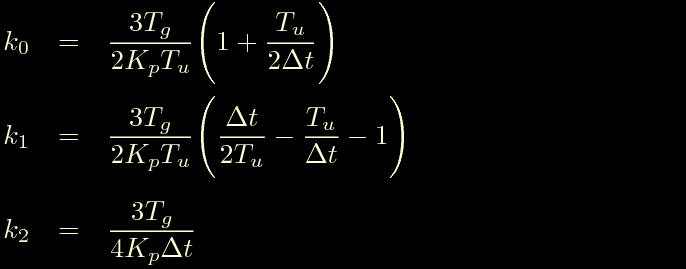
Se procediamo come in precedenza e bariamo per far sparire il tempo misurato in secondi, passando al tempo misurato in sample (parametri S), sostituendo:

Otteniamo le forme seguenti per i coefficienti del PID:
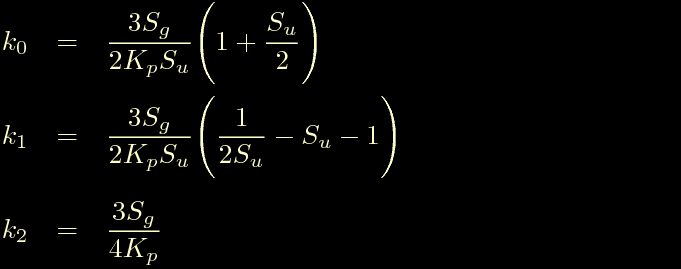
Assomigliano molto alle nostre, quindi un fondo di verita' dovrebbe esserci anche in questo regolatore, di fatto funzionava a dovere ed ha funzionato anche in diverse occasioni a seguire. Cerchiamo di districare la matassa e come in precedenza ricaviamo le coordinate polari degli zeri.

Cominciamo con la seconda delle due, da cui otteniamo:
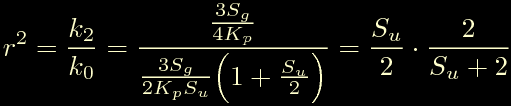
Saltando un po' di conti si arriva alla forma finale:
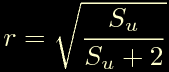
Ora e' il turno del coseno:
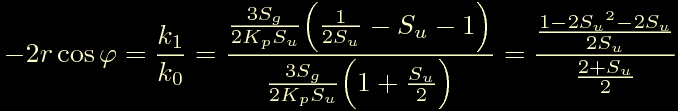
Anche qui saltando un po' di passaggi si ottiene:
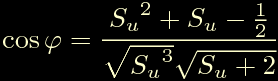
Perche' il coseno abbia senso, cioe' sia compreso tra 1 e -1 deve essere:
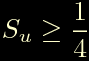
Ricapitolando le coordinate polari degli zeri dell'equazione sono le seguenti:

Tanto per incominciare, contrariamente a quello che tutti quanti si aspettavano, la posizione degli zeri dipende solo da Su; questo vuol dire che Sg ha qualche influenza sul guadagno del PID e non sulle caratteristiche integrale e/o derivativa. Vuol dire anche che non avremo tutti i gradi di liberta' di prima. Inoltre c'e' una nuova zona del piano che prima non veniva esplorata: per Su compreso tra 1/4 e circa 1/2 gli zeri si trovano in una zona che prima risultava inaccessibile, che cosa significa?
Ho tracciato il movimento degli zeri, sulla sinistra da solo e sulla destra in compagnia delle linee di riferimento precedenti: come si vede i nuovi zeri tagliano di traverso il dominio precedente, c'e' quindi da aspettarsi che l'unico parametro a disposizione faccia le veci di entrambi i precedenti, cioe' mentre esalta l'integrale riduce l'effetto derivativo e viceversa.
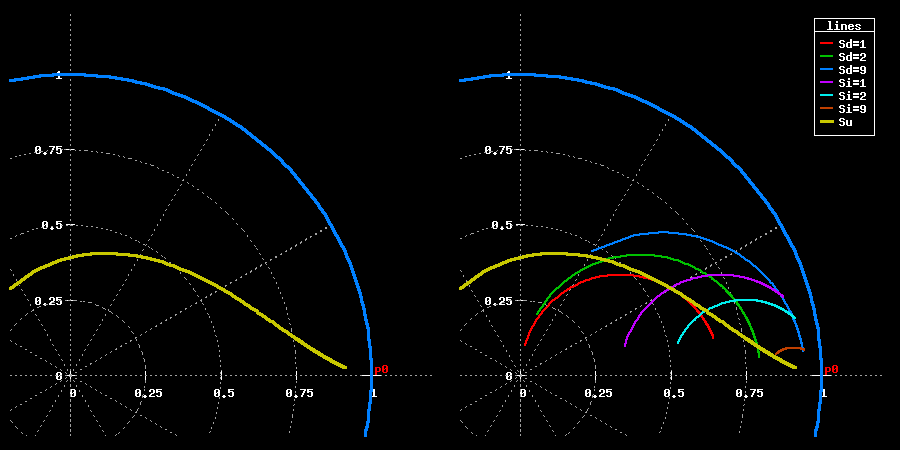
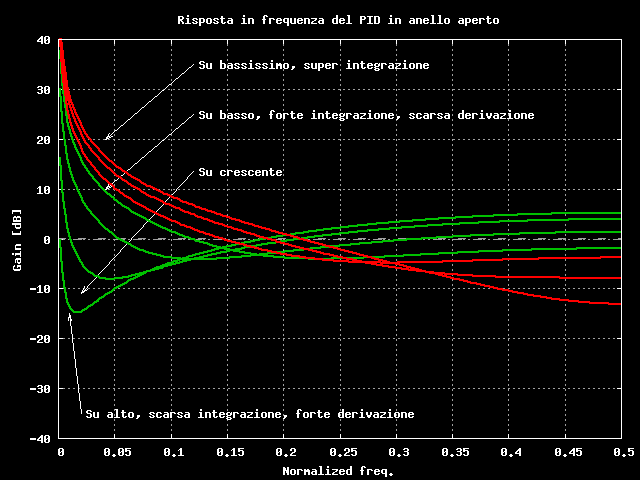
Per completare l'analisi ho voluto tracciare l'andamento in frequenza della risposta del PID, in verde gli andamenti per Su maggiore di 1/2, effettivemente mentre esalta la derivata ammazza l'integrale e viceversa. In rosso ho tracciato l'andamento nella zona vietata, questa sempbrerebbe una zona super integrale che potrebbe essere buona norma evitare il piu' possibile.
Download
Se qualcuno fosse interessato agli script per la generazione dei grafici e delle formule matematiche viste sopra, trova tutto qui.
| equ_pack.tar.gz | Pacchetto omnicomprensivo di tutti gli script. Gli script richiedono LaTeX e l2p. |