Trasformata z
Singolo zero
Calcolo di H(z)
Eq. alle diff. finite
Passa basso 1
Passa basso 2
Passa basso 3
La media come filtro
Camp. in frequenza
Casi notevoli
PID
Movimento
Trasformata z
La forma generale della trasformata z e' la seguente:
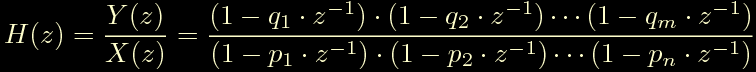
I punti q1, q2,... vengono detti zeri dell'equazione;
i punti p1, p2,... vengono detti poli dell'equazione.
Questa scrittura mette in evidenza i poli e gli zeri dell'equazione.
La disposizione dei poli e degli zeri nel piano complesso z determina la caratteristica del filtro digitale e il suo comportamento in frequenza.
Esistono due grandi famiglie di filtri digitali: FIR e IIR. Un filtro che contiene solo zeri si definisce FIR: in questo tipo di filtri l'uscita dipende, istante per istante, solo dall'ingresso e dalla storia di questo. Un filtro che contiene anche dei poli (o solo poli) si definisce IIR: in questi filtri l'uscita dipende, istante per istante, oltre che dall'ingresso e dalla sua storia anche dalla storia dell'uscita stessa.
Singolo zero
Vediamo alcuni esempi per capire meglio da che parte gira il fumo, consideriamo un caso molto semplice: un filtro che abbia un solo zero reale, cioe' del tipo:
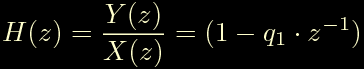
dove q1 e' un numero reale (positivo o negativo) e corrisponde chiaramente ad un punto del piano complesso z.
Ricordiamo che H(z) e' una funzione della variabile complessa z, quindi e' una superficie stesa sopra al piano complesso z. Detta in questi termini potrebbe sembrare complicato, in realta' basta pensare ad una funzione di due variabili z=f(x,y), altro non e' che una superficie stesa sopra ad un piano, il piano x, y appunto.
Nel nostro caso le cose sono leggermente piu' complicate: una funzione di variabile complessa potrebbe essere a sua volta complessa, in questo caso non sarebbe semplice farne un grafico; per nostra fortuna non siamo interessati al valore complesso di H(z), ma al modulo di H(z), il che semplifica oltre alla rappresentazione anche i conti.
Dunque ricapitolando vogliamo rappresentare la funzione modulo di
H(z), dove z e' una variabile complessa; il risultato
sara' quindi una superficie stesa al di sopra del piano complesso
z.
Ora posizioniamo il nostro zero sul piano complesso; scegliamo ad
esempio un valore negativo prossimo a -1, quello che si ottiene e' la
superficie seguente.
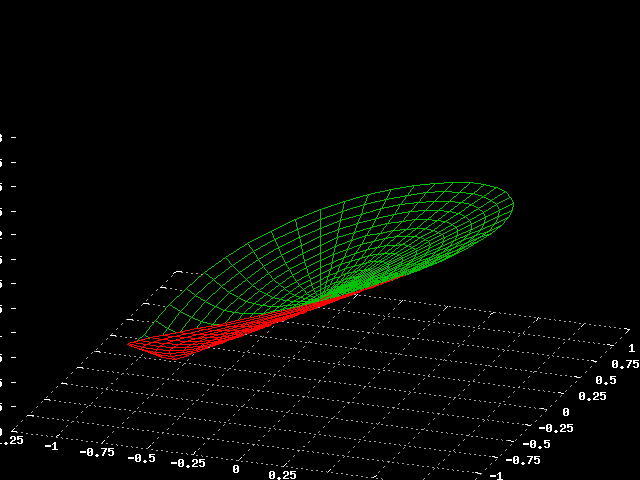
Funzione con uno zero reale.
Qui sotto si vede la posizione dello zero nel piano complesso.
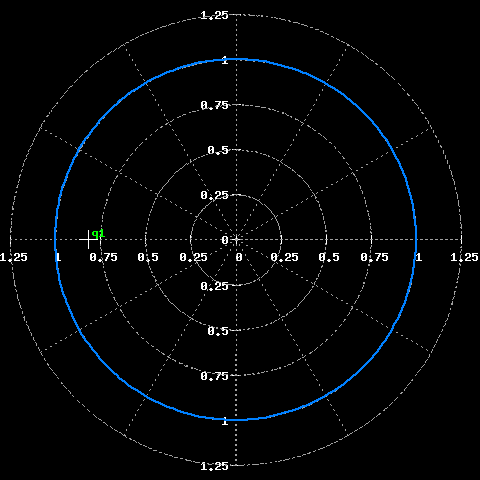
Posizione dello zero nel piano complesso.
Avrete notato che la superficie non viene calcolata per tutto il piano complesso, ma solo fino alla circonferenza unitaria; in effetti per i nostri scopi non ci interessa la superficie, ma solo il suo valore lungo la circonferenza unitaria.
Muovendoci solo lungo la circonferenza unitaria e calcolando la nostra H(z) solo su questo dominio, possiamo produrre un grafico planare come il seguente.
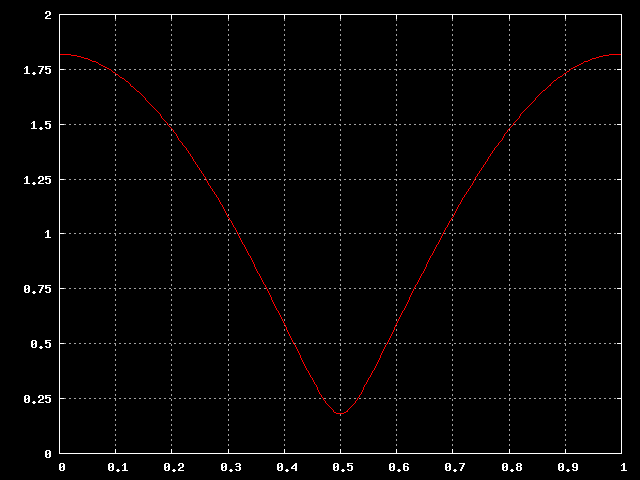
Risposta in frequenza del filtro digitale.
L'asse verticale non e' variato rispetto al grafico tridimensionale visto sopra, invece l'asse orizzontale e' completamente diverso: questo viene detto asse delle frequenze normalizzate, varia tra 0 e 1 ed e' periodico. Lo 0 corrisponde alla frequenza zero, o componente continua del segnale, l'1 corrisponde alla frequenza di campionamento del segnale, il punto 0.5 viene chiamato frequenza di Nyquist e corrisponde alla frequenza massima che si puo' trovare all'interno del segnale.
Chiaramente i punti di questo asse hanno una corrispondenza anche col
piano complesso: corrispondono ai punti dell'asse curvo che segue la
circonferenza unitaria partendo dal punto 1+j0 e girando in senso
antiorario. Il punto 0 dell'asse delle frequenze normalizzate
corrisponde col punto 1+j0 del piano complesso, il punto 0.5
corrisponde col punto -1+j0 del piano complesso ed infine il punto 1
dell'asse corrisponde nuovamente col punto 1+j0 del piano complesso.
Per chiarezza qui sotto riporto alcuni punti notevoli del piano
complesso.
Il grafico e' sempre simmetrico rispetto al punto 0.5 per segnali
reali.
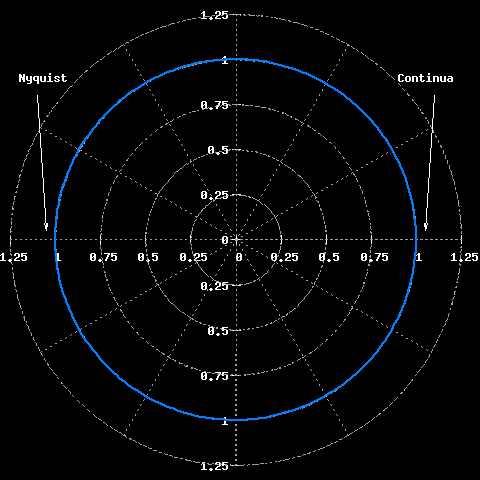
Punti notevoli del piano complesso z.
Calcolo di H(z)
Come si calcola H(z)?
Come si produce il grafico visto sopra?
Riprendiamo la forma generale della trasformata z.
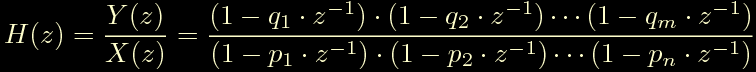
Abbiamo detto di essere interessati al modulo di H(z), quindi riscriviamola nella seguente forma:
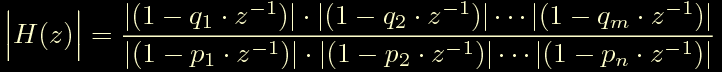
Ciascuno di questi puo' essere calcolato come il modulo della differenza tra il vettore z e il vettore q:
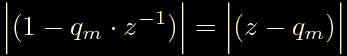
Il grafico seguente riassume il concetto: il modulo di H(z) viene calcolato come prodotto e quoziente delle distanze tra il punto z che corre lungo la circonferenza unitaria e i vari poli e zeri che sono stati posizionati sul piano complesso. Ci tengo a precisare che questo calcolo e' rigoroso e non e' affetto da approssimazioni di sorta.
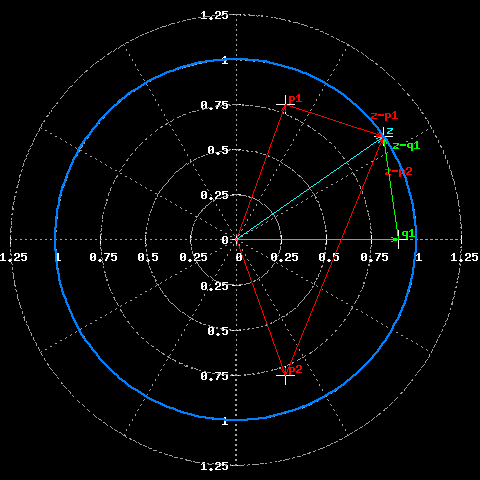
Calcolo del modulo di H(z).
In questo esempio risulta:
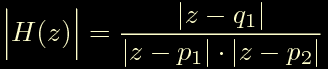
Senza inserire il grafico di H(z), mi limitero' ad osservare che il modulo di H(z) tende ad annullarsi in 1, mentre tende a divergere quando z passa davanti ai due poli complessi coniugati p1 e p2; e' appunto giocando con la posizione dei poli e degli zeri che si puo' sagomare a piacere la risposta in frequenza del filtro digitale.
Equazione alle differenze finite
Abbiamo visto come si scrive la trasformata z, abbiamo visto
che poli e zeri modificano la risposta in frequenza, quindi giocando
con le posizioni di questi possiamo sagomare il nostro filtro.
Supponiamo ora di aver trovato una risposta soddisfacente per i
nostri scopi, vogliamo quindi realizzare il filtro, come si fa?
Di fatto in tutto quello che abbiamo scritto fin'ora il segnale
d'ingresso non c'e', e nemmeno quello di uscita se guardiamo bene;
quindi cosa facciamo?
Dobbiamo produrre quella che viene chiamata equazione alle
differenze finite, cioe' un'equazione che esprima l'uscita del
filtro come funzione del segnale in ingresso.
Riprendiamo la forma generale della trasformata z:
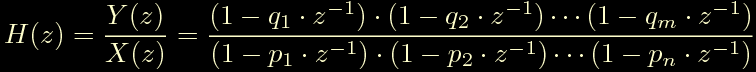
la riscriviamo spostando tutti i poli alla sinistra dell'uguale e tenendo tutti gli zeri sulla destra:
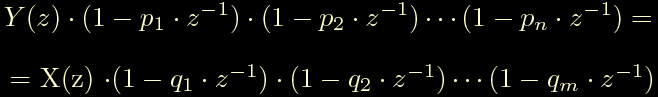
ora, mi dispiace dirlo, svolgiamo i calcoli ed eseguiamo tutti i prodotti; in questi casi lo sbiancamento dei capelli e' direttamente proporzionale al grado dell'equazione, ma con un po' di pazienza si arriva a qualcosa di questo tipo:
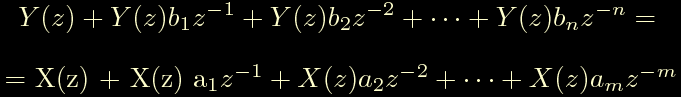
adesso basta ricordarsi di uno dei principi fondamentali della trasformata z: cioe' che moltiplicare per z^-1 equivale ad introdurre un ritardo temporale pari ad un campione. Con questa idea in testa riscriviamo l'equazione sostituendo Y(z) con y(k) e X(z) con x(k), ottenendo questa formula:
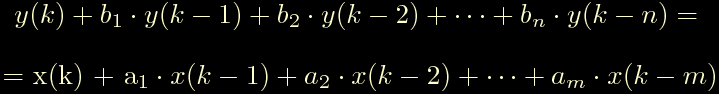
Questa e' quella che in gergo tecnico si chiama equazione alle differenze finite ed e' quello che ci serve per poter implementare il filtro digitale. Sembra incredibile, ma questa cosa realizza veramente la risposta in frequenza trovata in precedenza.
Passa basso 1
Supponiamo di voler realizzare un filtro passa basso.
Se proviamo ad avanzare una richiesta di questo tipo ad un ingegnere
veniamo immediatamente travolti da una serie di domande del tipo:
"Quanto deve essere larga la banda passante?", oppure:
"Quanto vale l'attenuazione in banda oscura?" e ancora
"Quanto e' larga la banda di transizione?".
Tutte domande a cui un ingegnere stesso potrebbe avere non pochi
problemi per rispondere.
Cerchiamo di affrontare il problema in modo meno serio, se fossimo in
grado di rispondere a domande di questo tipo probabilmente saremmo
gia' i maestri della trasformata z; pertanto non avremmo
bisogno di leggere queste pagine.
Decidiamo in modo del tutto arbitrario che il filtro deve
essere di tipo passa basso e poniamo un solo zero alla
frequenza di Nyquist, vediamo che cosa succede.
Partendo dall'equazione generale:
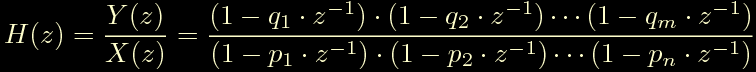
otteamo la seguente equazione, in cui abbiamo posto q1=-1:
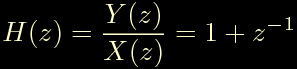
Per chiarezza marchiamo la posizione dello zero sul piano complesso:
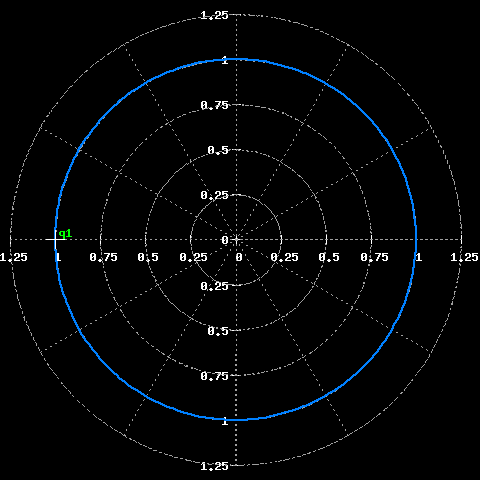
Posizione dello zero nel piano complesso.
Calcoliamo la risposta in frequenza ed otteniamo il seguente andamento:
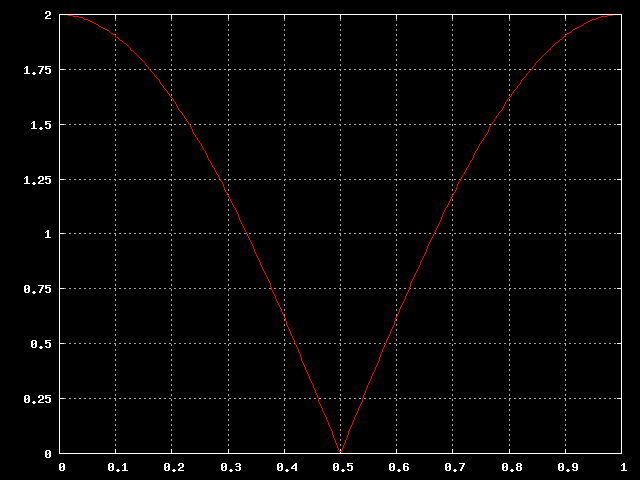
Risposta in frequenza del filtro.
L'asse verticale e' un numero puro che esprime il guadagno del filtro, questo perche' siamo ancora alle prime armi, in seguto l'asse verticale sara' espresso in dB, come fanno i veri ingegneri.
Notiamo che il guadagno si annulla alla frequenza di Nyquist,
era proprio quello che volevamo, quindi forse non siamo troppo
lontani dal traguardo. Notiamo anche che il guadagno in
continua vale 2; questa cosa potrebbe stupirci. Per questo fenomeno
esiste una spiegazione piuttosto singolare che gira per le aule
universitarie: la funzione modulo di H(z) tende normalmente a
comportarsi come un cuscino uniforme di altezza 1; posizionando degli
zeri nel piano complesso possiamo inchiodare in alcuni punti
la superficie a quota 0, ma di conseguenza il cuscino tende a
rigonfiare nelle zone libere dai chiodi.
Questa spiegazione e' tutt'altro che matematica ma rende molto bene
il concetto, anche la prima superficie tridimensionale che abbiamo
visto mostra proprio questo fenomeno.
Nessun problema comunque: in qualunque momento possiamo correggere
il guadagno del filtro senza alterare l'andamento in frequenza,
decidiamo ad esempio
dividere tutto per 2 per correggere il guadagno in continua:
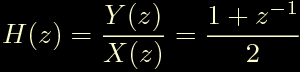
da questa ricaviamo l'equazione alle frequenze finite del filtro:
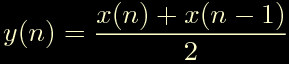
L'equazione alle differenze finite vista sopra potrebbe darci una
strana sensazione di deja vu: se la guardiamo bene notiamo che
questo filtro esegue la media tra l'ingresso attuale e il
precedente.
Ricalcoliamo la risposta in frequenza, questa volta utilizzeremo un
asse verticale in dB, giusto per complicare un pochino il
gioco.

Risposta in frequenza del filtro.
Osserviamo l'andamento della risposta n frequenza del filtro: abbiamo chiesto un guadagno unitario in continua e che fosse cancellata la frequenza di Nyquist e questo e' stato fatto. In tutti gli altri punto non abbiamo posto condizioni, quindi il filtro decide autonomamente come comportarsi. Questo concetto sta alla base dell'ordine del filtro: l'ordine del filtro e' dato dal numero di vincoli che vengono imposti, se volete dal numero di poli e zeri dell'equazione. Un filtro con molti vincoli puo' avere un andamento molto complicato, ma avra' anche un ordine molto alto, quindi richiedera' risorse computazionali superiori. Di fatto il dimensionamento di un filtro digitale e' sempre un trade-off tra le necessita' e le risorse disponibili.
Torniamo al nostro filtro e diciamo che abbiamo rimosso le alte frequenze dal segnale, per il momento ci basta e siamo soddisfatti di questo risultato.
Passa basso 2
Proviamo ad aggiungere altri due zeri al filtro visto in precedenza, vogliamo tenere giu' i rigonfiamenti del nostro cuscino; vediamo che cosa succede. Aggiungiamo 2 zeri complessi coniugati in 0+j e 0-j, esattamente a frequenza 0.25 (normalizzata). Questa la nuova situazione sul piano complesso:
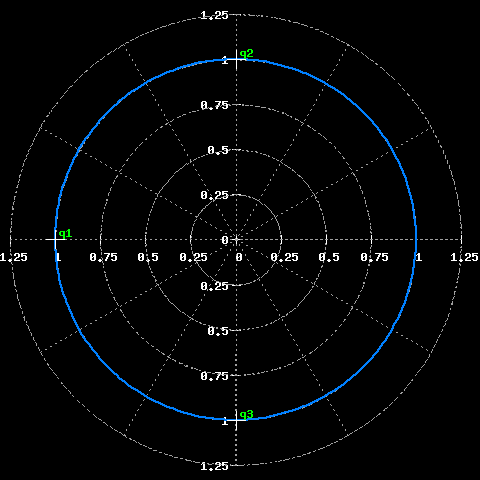
Posizione degli zeri nel piano z.
La trasformata z assume la seguente forma:
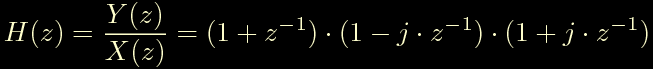
Come al solito calcoliamo la risposta in frequenza del filtro ed otteniamo il seguente andamento:
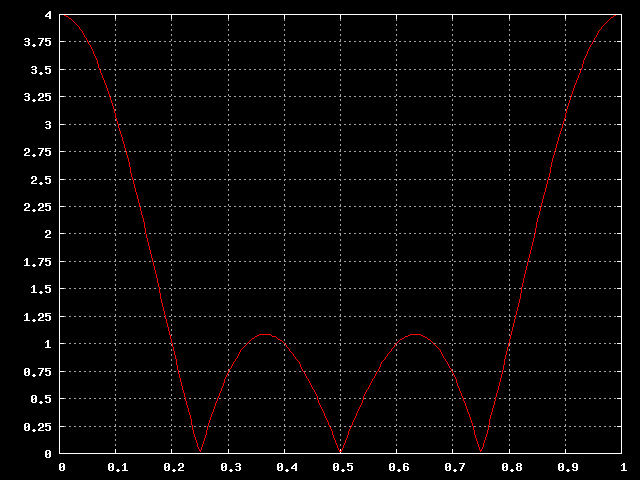
Risposta in frequenza del filtro.
Abbiamo ottenuto quello che cercavamo: il guadagno si azzera anche per la frequenza 0.25, a meta' strada tra la continua e la frequenza di Nyquist; come al solito il guadagno in continua e' schizzato verso l'alto ma abbiamo gia' visto che possiamo rimediare. Ora tentiamo di passare dalla trasformata z all'equazione alle differenze finite; svolgendo parte dei calcoli otteniamo:
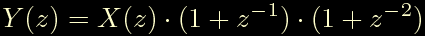
svolgendo tutte le moltiplicazioni sulla destra si ottiene:
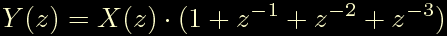
da cui ricaviamo l'equazione alle differenze finite:
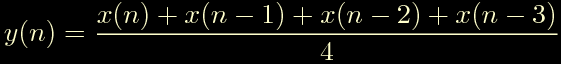
in cui il guadagno in continua e' gia' stato corretto.
A guardarla bene si direbbe che questo filtro esegua la media degli
ultimi 4 campioni in ingresso.
Visto che siamo ansiosi di sapere come filtra questo coso e di quanto
e' migliorato rispetto al precedente calcoliamo subito la risposta in
frequenza:
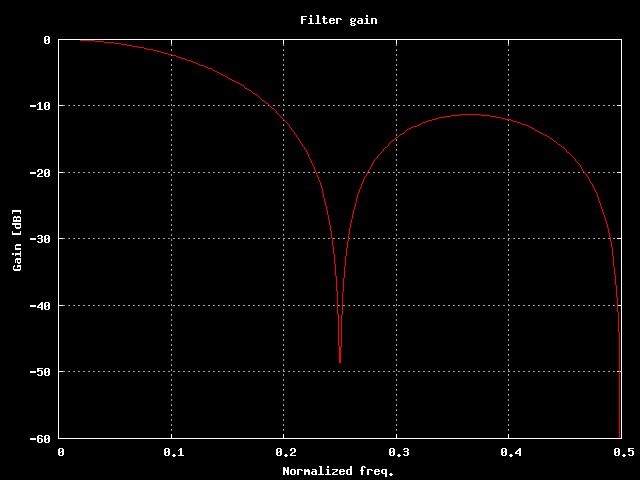
Risposta in frequenza del filtro.
Espresso in dB il grafico sembra meno confortante di quello lineare: in buona sostanza questo filtro lascia passare meta' della banda del segnale digitale ed ha una attenuazione in banda oscura di soli 10dB. Se volessimo utilizzarlo come filtro passa basso non otterremmo grandi risultati, e' comunque molto utile per eliminare frequenze indesiderate, suppondendo che il disturbo habbia proprio frequenza 0.25.
Passa basso 3
Visto l'andazzo adesso tiro ad indovinare: scommetto che se metto
altri 4 zeri lungo la circonferenza posizionati ogni 45 gradi ottengo
un filtro che esegue la media degli ultimi 8 campioni in ingresso.
Proviamo, gli zeri sono disposti in questo modo:
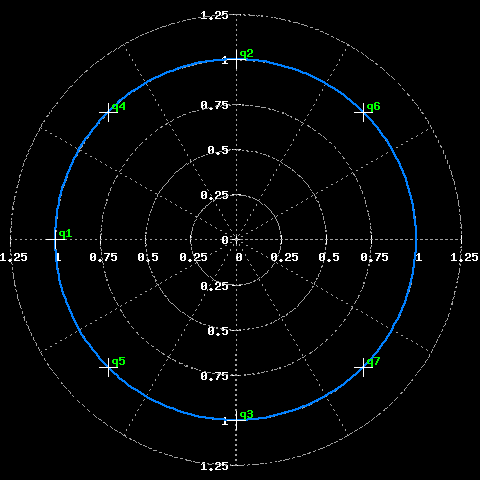
Posizione degli zeri nel piano complesso.
e la trasformata z assume la seguente forma:
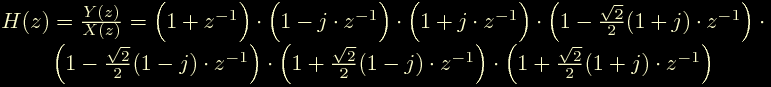
Questa la risposta in frequenza del filtro:
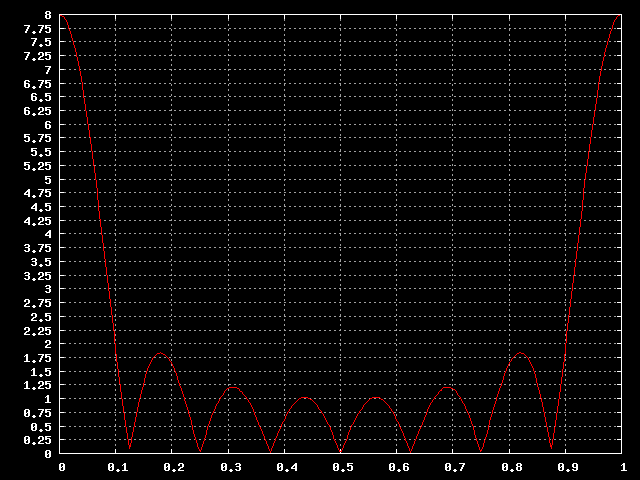
Risposta in frequenza del filtro.
Passiamo subito allo svolgimento dei calcoli, dalla trasformata vista sopra otteniamo, dopo una svalangata di conti:
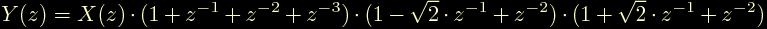
eseguendo i prodotti sulla destra si ottiene:
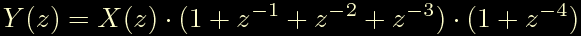
infine passiamo al dominio del tempo e correggiamo il guadagno in continua:
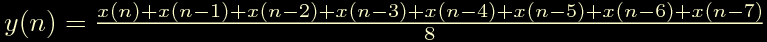
Questo conferma la nostra idea iniziale: questo filtro esegue
veramente la media degli ultimi 8 campioni in ingresso.
Vediamo come si modifica la risposta in frequenza:
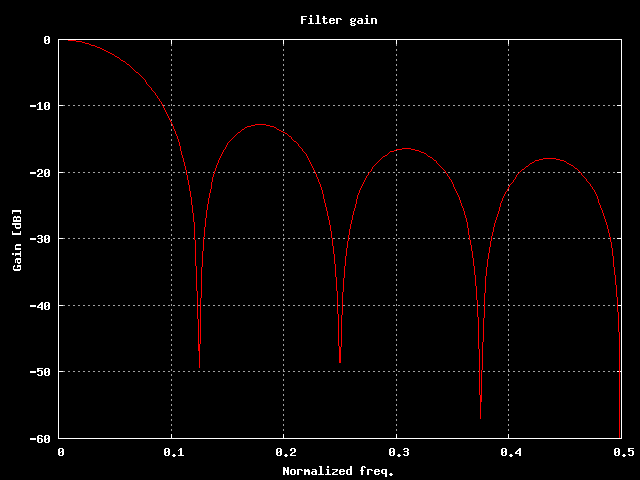
Risposta in frequenza del filtro.
La media come filtro
La cosa non era programmata, per uno strano scherzo del destino fin'ora abbiamo visto dei filtri che in un modo o nell'altro fanno la media degli ultimi N campioni in ingresso. Spingiamoci allora fino in fondo: si puo' usare la media per filtrare?
Una volta avevo un collega che sosteneva le mirabolanti proprieta' della media aritmetica quale filtro numerico. Ancora oggi sento spesso parlare di media mobile quale soluzione di tutti i mali. Prendiamo come assodato che la media e' un filtro, ma come filtra la media?
Almeno in parte abbiamo gia' risposto a questa domanda, ora possiamo aggiungere che la media aritmetica degli ultimi N campioni in ingresso e' quel filtro che calcola la prima riga di una serie di Fourier, la riga a frequenza zero. In sostanza la media e' un filtro che restituisce la componente continua presente nel segnale, tentando di escludere tutte le altre frequenze. Certo fin'ora non abbiamo escluso quasi niente dal segnale originale, ma aumentando il numero di campioni presenti nella media ci si spinge sempre di piu' verso la componente continua del segnale.
Visto che ci piace essere tecnici e le parole non ci soddisfano appieno, ecco alcuni grafici che mostrano come filtra la media.
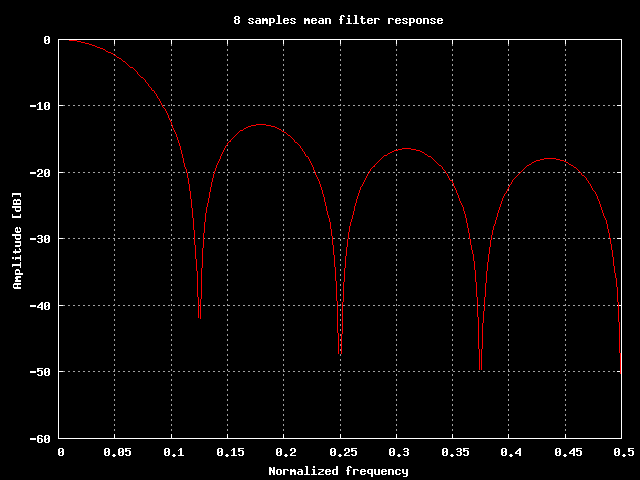
Risposta in frequenza di un filtro che media 8 campioni.
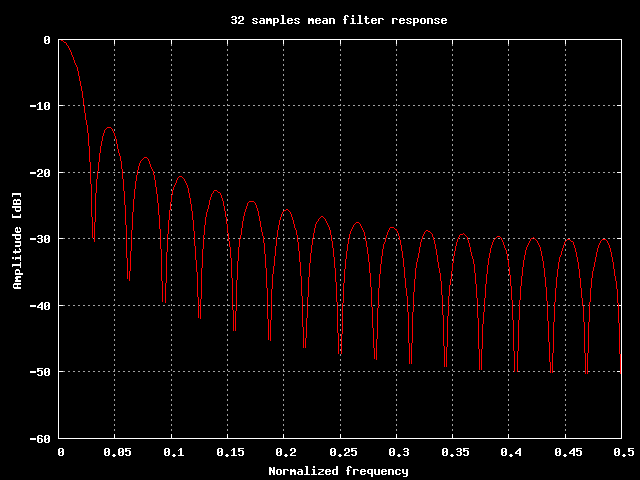
Risposta in frequenza di un filtro che media 32 campioni.
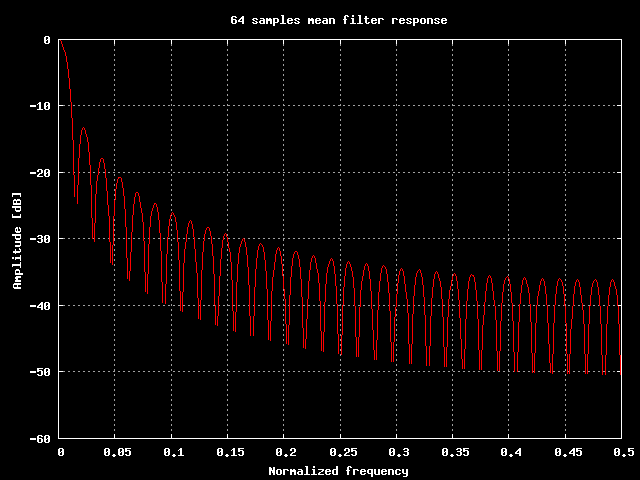
Risposta in frequenza di un filtro che media 64 campioni.
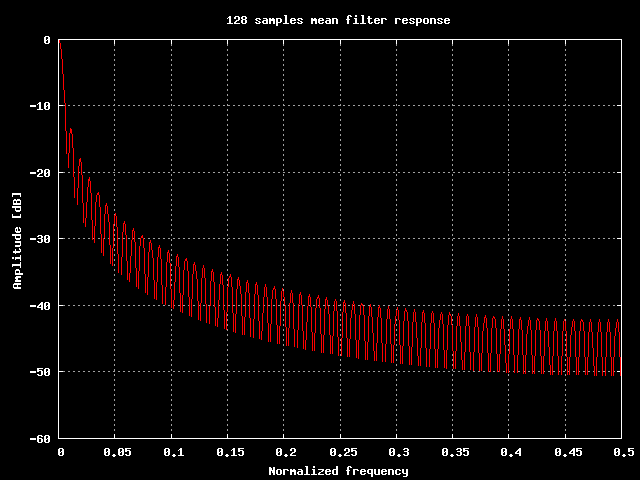
Risposta in frequenza di un filtro che media 128 campioni.
Il tuttp passa come un filtro tutti zeri che ha tanti zeri quanti i campioni che entrano nella media, equispaziati lungo la circonferenza unitaria, in cui manca lo zero in 1.
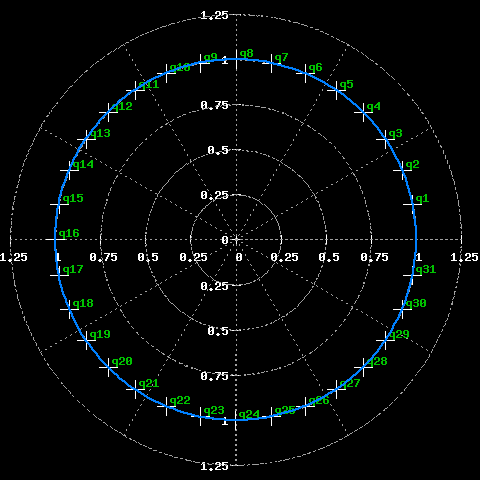
Disposizione degli zeri in un filtro che media 32 campioni.
La regola e' sempre la stessa: se i grafici sopra vi soddisfano, se la ricerca della componente continua era proprio quello che cercavate, allora questo e' il vostro filtro, altrimenti lasciate perdere la media.
Campionamento in frequenza
Vediamo ora un altro metodo per la sintesi dei filtri digitali: quello che viene definito campionamento in frequenza.
Consideriamo una generica equazione alle differenze finite di un filtro FIR di ordine N, questa e' data dalla somma degli ultimi N campioni in ingresso al filtro ciascuno moltiplicato per un opportuno coefficiente. L'equazione assume quindi un aspetto di questo tipo:
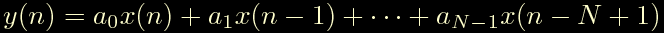
Il numero N di coefficienti definisce l'ordine del filtro e non ha niente a che fare con l'ordine dei filtri analogici. Come vedremo tra poco e' molto facile avere filtri digitali di ordini elevati.
L'ordine del filtro definisce anche il suo costo computazionale, infatti un filtro di ordine N richiede N moltiplicazioni per produrre l'uscita, questo e' un fattore di cui tenere ben presente nel progetto dei filtri digitali: il filtro che abbiamo in mente potrebbe richiedere una potenza di calcolo di cui non disponiamo o che sarebbe troppo costosa.
Procediamo come al solito facendo qualche esperimento e vediamo che cosa succede. Fissiamo l'ordine del nostro filtro a N=8. La conseguenza immediata di questo gesto e' quella di suddividere l'asse delle frequenze normalizzate (da 0 a 1) in 8 spazi uguali. Per ciascuno dei punti individuati sull'asse delle frequenze scegliamo un valore di ampiezza della risposta in frequenza, avremo i valori di ampiezza: X0, X1, X2, X3, X4, X5, X6 e X7.
A causa della circolarita' dell'asse delle frequenze e della natura reale dei segnali in ingresso e in uscita dal filtro stesso, non possiamo scegliere 8 valori differenti, ma alcuni di questi saranno legati tra loro. In particolare siamo costretti a scegliere: X1=X7, X2=X6, X3=X5. A parte questi vincoli indissolubili possiamo scegliere i valori numerici come meglio crediamo (pur che siano reali). Poniamo ad esempio:
| X0 | 1.00 |
| X1 | 0.90 |
| X2 | 0.30 |
| X3 | 0.05 |
| X4 | 0.00 |
| X5 | 0.05 |
| X6 | 0.30 |
| X7 | 0.90 |
Il grafico qui sotto mostra la posizione de nostri 8 punti:
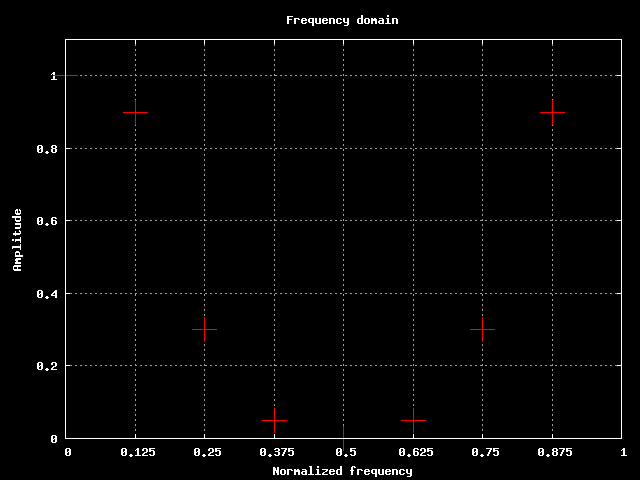
Posizione dei punti scelti nel campionamento in frequenza.
Questi punti rappresentano un vincolo per la risposta in frequenza del filtro: il filtro che costruiremo avra' una risposta in frequenza che passera' per i punti scelti. Purtroppo non abbiamo poteri al di fuori di questi 8 punti, abbiamo gia' fatto questo discorso: l'ordine del filtro definisce quanti vincoli riusciamo ad imporre sulla risposta del filtro stesso.
Ok, per quello che ne sappiamo i valori scelti sopra vanno benissimo,
e' proprio il filtro dei nostri sogni, come si procede ora?
Tenendo i coefficienti Xk nell'ordine in cui sono scritti
sopra antitrasformiamo secondo Fourier e troviamo la sequenza
di coefficienti xn.
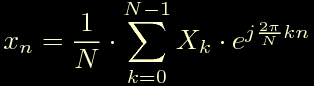
Questi sono i nostri coefficienti:
| x0 | 0.4375 |
| x1 | 0.2753 |
| x2 | 0.0500 |
| x3 | -0.0253 |
| x4 | -0.0375 |
| x5 | -0.0253 |
| x6 | 0.0500 |
| x7 | 0.2753 |
Questi coefficienti non possono essere utilizzati cosi' come sono,
sarebbe troppo facile!
Conviene riordinarli in modo da soddisfare la relazione di causalita'
del filtro.
Riordiniamo i coefficienti in questo modo:
| a0 | x4 | -0.0375 |
| a1 | x5 | -0.0253 |
| a2 | x6 | 0.0500 |
| a3 | x7 | 0.2753 |
| a4 | x0 | 0.4375 |
| a5 | x1 | 0.2753 |
| a6 | x2 | 0.0500 |
| a7 | x3 | -0.0253 |
Il primo coefficiente, a0, e' il coefficiente che moltiplica
il campione attuale, mentre a7 e' il coefficiente che
moltiplica il campione piu' vecchio presente nella coda del
filtro.
Questo significa che il nostro filtro avra' la seguente equazione
alle differenze finite:
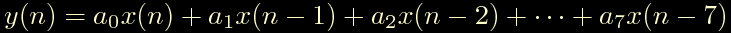
In questo caso abbiamo gia' ottenuto l'equazione del filtro, quindi potremmo partire subito ad applicarlo, ma non sappiamo bene come si comporti al di fuori dei punti scelti. Se facesse cose strane?
Dati i coefficienti del filtro del dominio del tempo, e' possibile
calcolare il comportamento completo in frequenza.
In formule abbiamo che:
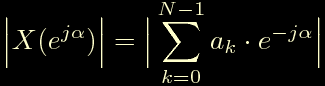
La formula calcola il modulo di H(z) per un alfa assegnato, dando per scontato che ci stiamo muovendo lungo la circonferenza unitaria ci basta indicare un angolo alfa. Spazzolando tutta la circonferenza unitaria otteniamo la risposta completa. Il risultato si puo' vedere qui sotto.
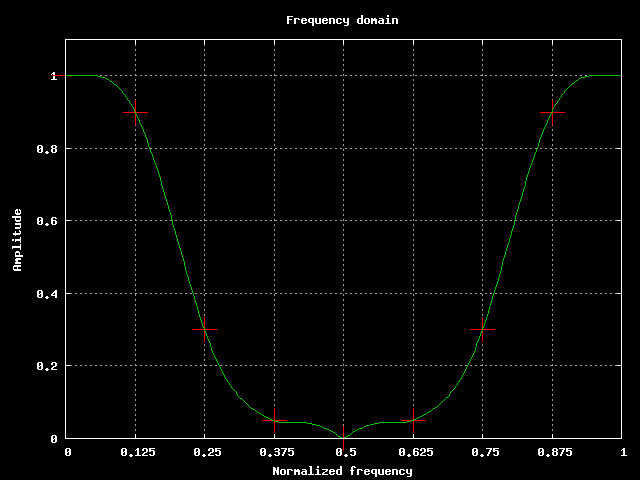
Posizione dei punti scelti nel diagrama delle frequenze.
Ci tengo a farvi notare che la risposta in frequenza passa proprio
per i punti che avevamo fissato.
Come al solito facciamo il grafico in dB perche' siamo
bastardi dentro.
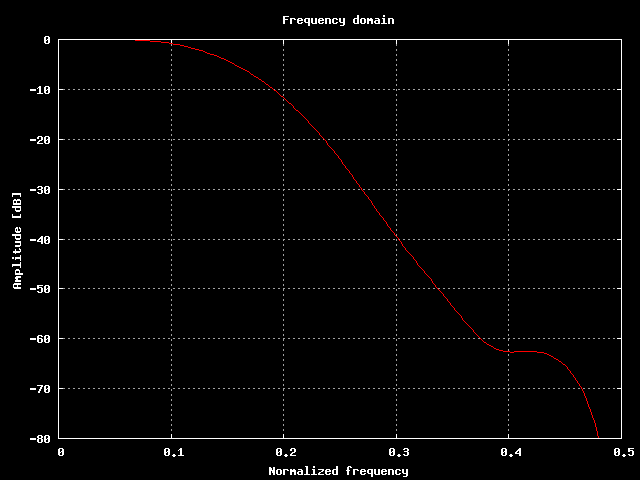
Posizione dei punti scelti nel diagrama delle frequenze.
L'andamento della curva potrebbe sembrare alquanto bizzarro, non lo nego, ma dopo tutto siamo partiti scegliendo dei punti quasi a caso.
Proviamo a spostare leggermente alcuni punti, vorremmo ottenere
un filtro passa basso con
un'attenuazione di almeno 60dB in banda oscura. Per ottenere questo
portiamo a 0 tutti i punti intorno alla frequenza di
Nyquist.
Scegliamo i punti in questo modo:
| X0 | 1.00 |
| X1 | 0.63 |
| X2 | 0.03 |
| X3 | 0.00 |
| X4 | 0.00 |
| X5 | 0.00 |
| X6 | 0.03 |
| X7 | 0.63 |
Trasformiamo come visto in precedenza e riordiniamo i coefficienti trovati per soddisfare i requisiti di causalita' e otteniamo i seguenti coefficienti:
| a0 | x4 | -0.0250 |
| a1 | x5 | 0.0136 |
| a2 | x6 | 0.1175 |
| a3 | x7 | 0.2364 |
| a4 | x0 | 0.2900 |
| a5 | x1 | 0.2364 |
| a6 | x2 | 0.1175 |
| a7 | x3 | 0.0136 |
Calcoliamo il comportamento in frequenza e troviamo il seguente andamento:
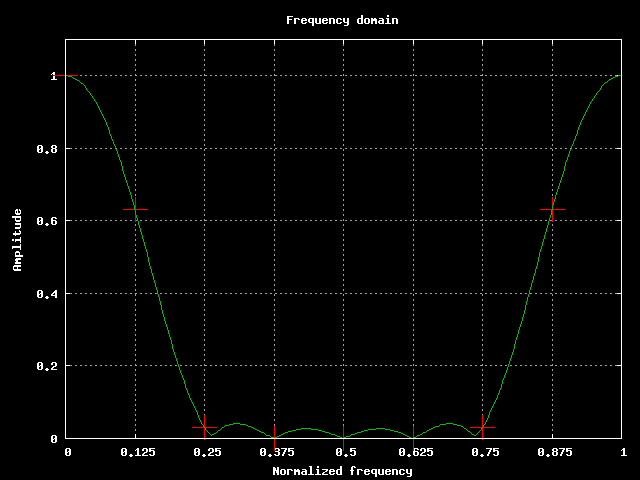
Andamento della risposta in frequenza.
Per finire calcoliamo la risposta in dB e ottenamo il seguente andamento:
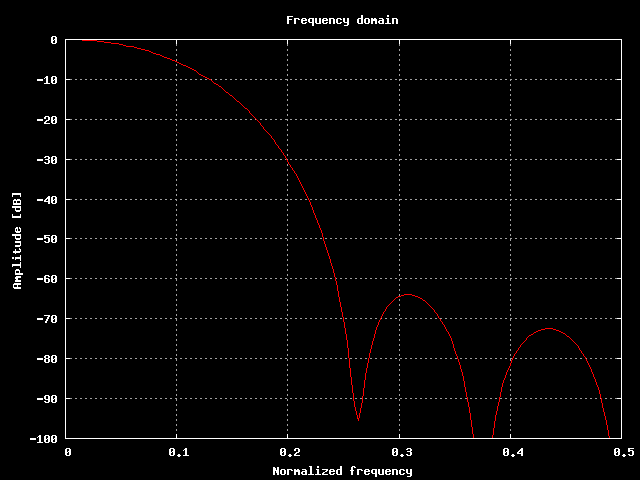
Andamento della risposta in frequenza.
Questo filtro e' sicuramente un interessante passa basso.
Casi notevoli
Visto che alcuni casi particolari tornano spesso nella pratica di tutti i giorni, riporto di seguito le equazioni alle differenze finite di questi casi particolari.
Uno zero reale

Due zeri reali
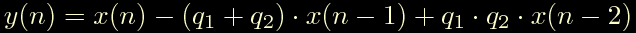
Due zeri complessi coniugati
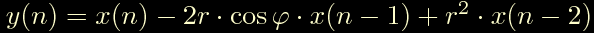
Uno zero reale + due zeri complessi coniugati
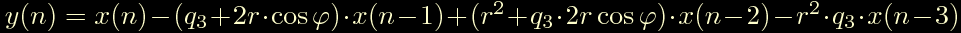
Un polo reale
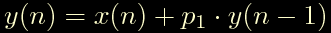
Due poli reali
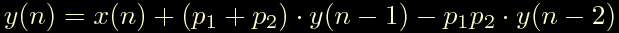
Due poli complessi coniugati
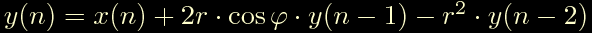
Un polo reale + due poli complessi coniugati
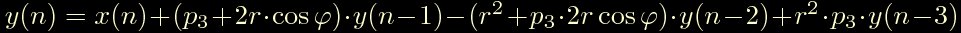
Un polo reale + uno zero reale
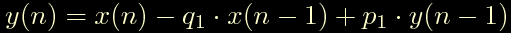
Un polo reale + due zeri complessi coniugati
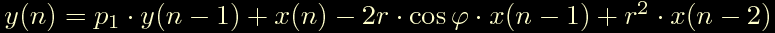
Uno zero reale + due poli complessi coniugati
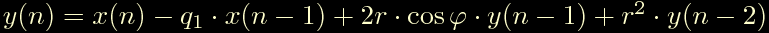
PID
Tra i sistemi di controllo piu' diffusi al mondo troviamo il famoso controllore PID, la sigla sta per: Proporzionale, Integrale, Derivativo. Smanacciando opportunamente con i coefficienti e' possibile adattarlo a quasi qualsiasi sistema da porre sotto controllo. Vediamo come si realizza un PID digitale.
Movimento
Una curiosita' quasi accademica: e' possibile mimare un movimento che
sembri naturale attraverso un filtro digitale?
Sembra che la risposta sia si, se qualcuno fosse interessato puo'
seguire l'argomento
qui.
Download
Se qualcuno fosse interessato agli script per la generazione dei grafici e delle formule matematiche viste sopra, trova tutto qui.
| buildequ | Bash script per la generazione delle equazioni contenute in queste pagine, richiedono LaTeX e l2p. |
| buildequ2 | |
| buildequ3 | |
| buildgrp.tar.gz | Bash script per la generazione di tutti i grafici contenuti in queste pagine, richiede gnuplot. |
| buildgrp_2.tar.gz |